有一個 $N \times M$ 的棋盤,裡面有一些障礙物,其餘格子是空地,障礙物以 # 表示、空地以 . 表示,現在在一格空地倒水,每過一秒,每一個有水的格子都會流水到它上、下、左、右本來沒有水的格子,求每個空地格子幾秒後會有水。
條件限制
- $N,M \leq 1000$
我們先直接看看流水過程的示意圖:
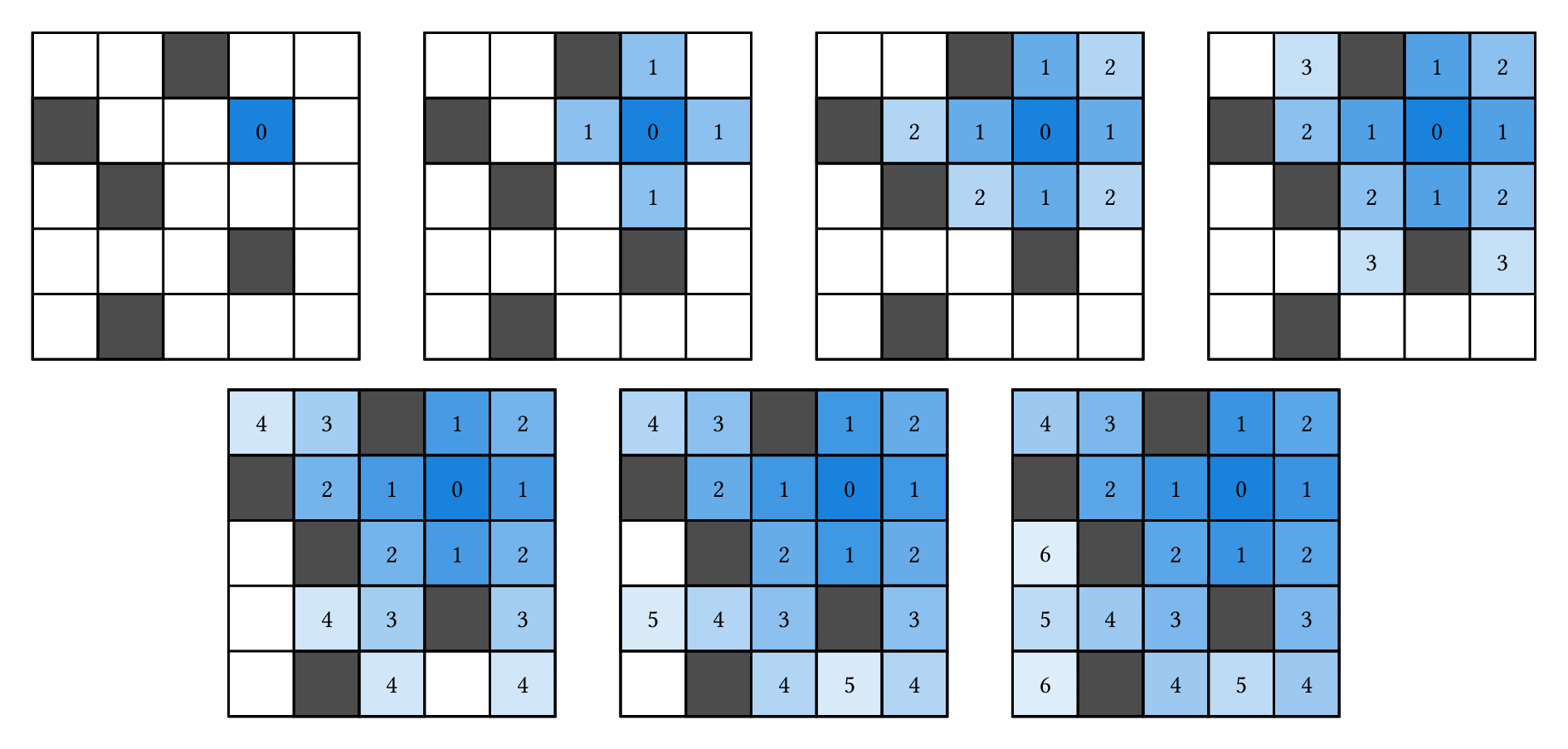
當水在往外擴張的時候,那些「有流水到新的格子」的格子,肯定是本來有水的最外圈格子,而這些最外圈格子,就是上一秒才有水的格子,畢竟如果更早就有水了,它早就流水到隔壁的格子了。也就是說,流水的過程是一圈一圈擴散出去的,那些答案是 $x$ 的格子,再往外擴散一格就是答案是 $x+1$ 的格子。
直接寫程式模擬這個流程的話,大致上就是先讓起點格子的答案是 $0$,接下來讓答案是 $0$ 的格子往旁邊流水,本來沒水的格子答案就是 $1$,然後讓所有答案是 $1$ 的格子往旁邊流水,新格子的答案是 $2$,再讓答案是 $2$ 的格子往旁邊流水……如此重複下去,直到某一輪裡面沒有再流到新的格子為止。
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1000;
string board[MAXN + 2];
int ans[MAXN + 2][MAXN + 2];
using pii = pair<int, int>;
pii dir[4] = {pii(-1, 0), pii(1, 0), pii(0, -1), pii(0, 1)};
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
int n, m, si, sj; // 起點是 (si, sj)
cin >> n >> m >> si >> sj;
for (int i = 1; i <= n; i++) {
cin >> board[i];
board[i] = '#' + board[i] + '#';
}
board[0] = board[n + 1] = string(m + 2, '#');
for (int i = 1; i <= n; i++)
fill(ans[i] + 1, ans[i] + m + 1, -1);
// ans[i][j] = -1 代表 (i, j) 目前沒有水
ans[si][sj] = 0;
// 剛剛新流到水的格子
vector<pii> last = {pii(si, sj)};
// last 裡面的格子是答案為 t 的格子
for (int t = 0; t <= n * m; t++) {
// 流出去的格子,答案是 t + 1
vector<pii> nxt;
for (auto [x, y] : last) {
for (auto [dx, dy] : dir) {
int nx = x + dx, ny = y + dy;
if (board[nx][ny] == '#' || ans[nx][ny] != -1) continue;
ans[nx][ny] = t + 1;
nxt.emplace_back(pii(nx, ny));
}
}
last = nxt;
}
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
cout << ans[i][j] << " \n"[j == m];
// 輸出 -1 代表水流不到
}
跟在深度優先搜尋提到的迷宮找路徑一樣,在一個棋盤上做事的時候,可以直接在外面加一圈障礙物以避免戳到棋盤外面。
在這個程式碼中,我們開了一個暫時的 vector nxt 來存這一輪新流到、下一輪要往外流的格子,其實這裡可以寫得更精簡一點,我們可以不用明確的一輪一輪地處理,因為我們根本就是做完本來 last 裡的格子之後,馬上緊接著處理 nxt 裡的格子,再處理它得到的 nxt 的格子、……,其實這根本就是一個被我們砍成兩半的 queue,直接用 queue 寫的話就變成:
queue<pii> q; // q 的前面一段會是本來寫法的 last、後面是 nxt
ans[si][sj] = 0;
// 對應到本來的 last = {pii(si, sj)}
q.push(pii(si, sj));
while (!q.empty()) {
auto [x, y] = q.front();
q.pop();
for (auto [dx, dy] : dir) {
int nx = x + dx, ny = y + dy;
if (board[nx][ny] == '#' || ans[nx][ny] != -1) continue;
ans[nx][ny] = ans[x][y] + 1;
// 對應到本來的 nxt.emplace_back(pii(nx, ny))
q.push(pii(nx, ny));
}
}實際上做出的事情和前面分成兩個 vector 的版本一模一樣。
因為一個格子只會成為「新的有水的格子」最多一次,因此時間複雜度是 $O(NM)$。
我們已經知道要怎麼用深度優先搜尋找一條在迷宮裡從起點到終點的路徑了,但如果我們要的是最短路徑的話呢?DFS 走出來的路有可能非常迂迴,比最短路徑還要長很多。
直接找到路徑可能有一點困難,我們先想想看怎麼知道最短路徑要走幾步。從起點走 1 步能到的格子是起點周圍的格子、走 2 步能到的格子就是那些走 1 步可以到的格子再往外走一格……這不就是我們剛剛的流水問題嗎?從起點倒一桶水,水流到終點要花幾秒,就是最短路徑需要幾步。
那要怎麼真的找到那條路徑呢?其實也很簡單,只要記錄每一格水是從哪裡流過來的,從終點往源頭追溯,最後一定會追回到起點,這條流水的路徑就是最短路徑了。
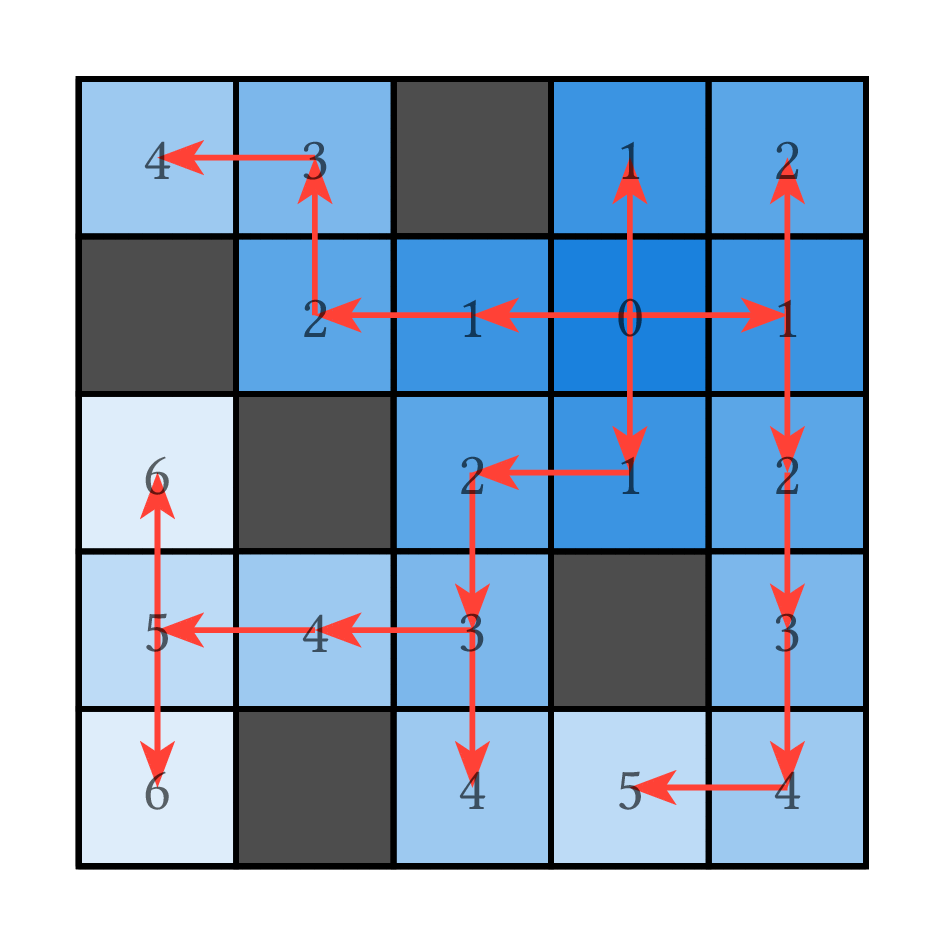
我們剛才做的事情被稱為廣度優先搜尋(Breadth-First Search),聽起來跟深度優先搜尋(DFS)很像,以走迷宮舉例,DFS 會優先往目前還沒走過的地方走,直到無處可走為止,因此 DFS 是優先往深處走,而 BFS 則會一圈一圈地擴大走到的範圍,讓已經走到的區域越來越廣。跟 DFS 相比,BFS 最大的特性是會按照每個地方跟起點的距離順序搜尋,以走迷宮來說就是離起點越近的格子,就會越早被走到。
既然 BFS 跟 DFS 一樣都能拿來走迷宮,那 BFS 是不是也像 DFS 一樣能拿來暴力搜尋呢?答案是可以,之前我們用 DFS 解決過這個問題:
給 $n$ 個正整數 $a_1,a_2,\dots,a_n$ 和一個數字 $S$,請列出所有 index 的集合 $i_1,i_2,\dots,i_k$,滿足 $a_{i_1}+a_{i_2}+\dots+a_{i_k} \leq S$。輸出的每一行代表一個集合,將集合中的數字 index 由小到大輸出,不同集合可以用任意順序輸出。
條件限制
- $n \leq 100$
- 保證答案個數 $\leq 10^4$。
在用 DFS 的時候,我們的作法是先決定第 1 個數字要不要選、再決定第 2 個數字要不要選、……,直到決定完每一個數字要不要選為止,最後用一個怪怪的順序枚舉出了所有總和不超過上限 $S$ 的集合。假設我們今天想要按照集合的大小,由數字少的集合到數字多的集合枚舉,那就很適合用「會保持從起點出發的距離順序」的 BFS 了,這裡的「起點」就是集合最少的空集合,然後我們要從一個已經搜尋到的集合找出更多集合,方法是每次往集合裡多加一個數字。
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 100;
int n;
long long S;
int a[MAXN];
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
cin >> n >> S;
for (int i = 1; i <= n; i++) cin >> a[i];
queue<vector<int>> q;
q.push(vector<int>()); // 起點是空集合
while (!q.empty()) {
vector<int> now = q.front(); // 目前我們找到的集合
q.pop();
// 哪些數字在這個集合裡,防止等一下重複拿到
vector<bool> use(n + 1);
int sum = 0; // 目前集合裡數字的總和
for (int i = 0; i < int(now.size()); i++) {
sum += a[now[i]];
use[now[i]] = true;
if (i > 0) cout << " "; // 順便輸出
cout << now[i];
}
cout << "\n";
for (int i = 1; i <= n; i++) {
if (use[i]) continue; // 這個數字已經在集合裡就不要拿
if (sum + a[i] > S) continue; // 總和太大就不要拿
vector<int> nxt = now;
nxt.emplace_back(i);
sort(nxt.begin(), nxt.end()); // 保持一下排序,也可以用 insert
q.push(nxt); // 放進 queue 裡等等處理
}
}
}
BFS 的實作核心就是用一個 queue 放我們還未處理過的東西,每次新找到一個集合,就把它放進 queue 裡,然後不斷從 queue 裡面拿出一個集合,再從它找出新的集合。這對應到剛才流水問題的例子中,每找到一個還沒有水的格子,就把它放進 queue 裡,然後不斷從 queue 裡拿出一個還沒往外流水過的格子,從它繼續往外流。
不過這個實作有一點問題,如果輸入
4 10
1 4 6 8輸出會是
(一個空行)
1
2
3
4
1 2
1 3
1 4
1 2
2 3
1 3
2 3
1 4出現了重複的集合!這是因為我們並沒有避免找到同樣的集合,例如我們可以往 $\{1\}$ 裡面多加一個數字得到 $\{1,2\}$,也可以往 $\{2\}$ 裡面多加一個數字得到 $\{1,2\}$。剛才的流水問題不會遇到這件事,是因為我們有避免把一個已經有水的格子再放進 queue 裡面(也就是如果 ans[nx][ny] != -1 就不處理),這裡也可以用類似的方法解決,像是在外面開一個 set<vector<int>> 儲存已經找到過、放進 queue 裡的集合,然後每次搜尋時,先確定新集合沒有出現在這個 set 中,才把它加進 queue。
注意這裡「是否已經搜尋到」的檢查是針對「是否有放進 queue 裡面過」的,而非「是否已經從 queue 拿出來處理過」,雖然要這樣做也不是不行,不過這樣無意義地被放進 queue 裡的東西會比較多,白白浪費時間和記憶體。不小心混用這兩種作法是一個常見的 bug,這兩個作法各自是正確的:
- 放進 queue 前檢查是否已經找到、放進 queue 的同時標記已經找到了。
- 拿出 queue 的時候先檢查是否已經處理過,沒處理過才進行處理,然後標記成已經處理過。
如果不小心寫成「拿出 queue 的時候標記成已經處理過、放進 queue 的時候先檢查是否已經處理過」,因為拿出 queue 的時候並沒有檢查是否有被處理過,它又現在才被標記成已處理,可能早就已經被放進 queue 裡好幾次了,這樣會造成同個東西被重複處理。
像是如果不小心把流水問題的程式碼寫成這樣,就會有這個問題,讀者可以自己實驗看看第 9 行的 cerr 是不是會輸出重複的格子。
// vst[i][j] = (i, j) 是否被處理過
queue<pii> q;
ans[si][sj] = 0;
q.push(pii(si, sj));
while (!q.empty()) {
auto [x, y] = q.front();
q.pop();
vst[x][y] = true; // 標記成已處理
cerr << x << " " << y << "\n";
for (auto [dx, dy] : dir) {
int nx = x + dx, ny = y + dy;
// 已經處理過的不要放進 queue
if (board[nx][ny] == '#' || vst[nx][ny]) continue;
ans[nx][ny] = ans[x][y] + 1;
q.push(pii(nx, ny));
}
}記錄已經搜尋到的集合是一種方法,不過這題有更簡單的解決方式:只要我們放進集合裡的數字編號都越來越大,那肯定不會枚舉到重複的集合,也就是我們每次搜尋的方式是「找到下一個要選擇的數字」,而選擇數字的順序必須按照編號,就像之前用 DFS 時我們是從第一個數字決定到最後一個,只是寫法有一點不一樣而已。
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 100;
int n;
long long S;
int a[MAXN];
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
cin >> n >> S;
for (int i = 1; i <= n; i++) cin >> a[i];
queue<vector<int>> q;
q.push(vector<int>()); // 起點是空集合
while (!q.empty()) {
vector<int> now = q.front(); // 目前我們找到的集合
q.pop();
int sum = 0; // 目前集合裡數字的總和
for (int i = 0; i < int(now.size()); i++) {
sum += a[now[i]];
if (i > 0) cout << " "; // 順便輸出
cout << now[i];
}
cout << "\n";
// 只能加入編號更大的數字
for (int i = now.empty() ? 1 : now.back() + 1; i <= n; i++) {
if (sum + a[i] > S) continue;
vector<int> nxt = now;
nxt.emplace_back(i); // 不用排序了!
q.push(nxt);
}
}
}
這樣輸出就會自然是:
(一個空行)
1
2
3
4
1 2
1 3
1 4
2 3既沒有重複的集合,也按照我們要求的按照數字少到多列出了所有答案。
BFS 跟 DFS 看起來可以做到的事情差不多,都可以走迷宮、都可以枚舉東西,總的來說,他們的功能都是搜尋,走迷宮是搜尋可以走到的地方、暴力枚舉就是搜尋要枚舉的東西,聽起來他們能做到的事情一樣,只是搜尋出東西的順序不一樣而已。
在某些狀況,確實兩者都行得通、沒有太大的差別,例如單純只是要找迷宮裡起點可以走到的格子,沒有要求要找最短路徑的話,BFS 跟 DFS 同樣都可以做到這件事,時間、空間複雜度都是 $O(\text{迷宮大小})$,不過並不是所有例子都是這樣。
在枚舉物件時使用 BFS 通常會比較麻煩,首先是 DFS 的遞迴過程用在暴力枚舉相對直覺許多,通常會比較好寫,再來是 BFS 需要把還未處理過的物件放在 queue 裡面,而 DFS 通常只要存下目前搜尋到的物件的長相以及遞迴的 stack 即可,例如在枚舉集合時,DFS 只要存下集合裡面至多 $n$ 個數字,BFS 的 queue 裡卻可能有高達 $O(2^n)$ 個集合,這種時候如果沒有特別的需求,用 DFS 是比較適合的。走迷宮不會這樣是因為一個格子也就用兩個 int 表示就好了,雖然 BFS 的 queue 可能需要存下 $O(\text{格子數量})$ 個格子,但 DFS 的遞迴 stack(是一條從起點走到目前格子的路徑)也同樣可能是一條這麼長的路,所以它們才會有一樣的空間複雜度。
不過,如果要找的是最短路徑,那這是 DFS 沒有的功能,用 BFS 就對了。
給一個 $n \times m$ 的迷宮,有些格子是障礙物,其他是空地,求這個迷宮裡有幾個連通的區域。
條件限制
- $n,m \leq 1000$
給一個左下角格子點座標是 $(0,0)$、右上角是 $(99,99)$ 的棋盤,棋子放在格子點上,有些格子點上有障礙物,現在有一個棋子每次可以走 $1 \times 3$,給這個棋子的起點和所有障礙物位置,求它要走到指定終點最少要幾步。
條件限制
- $n \leq 1000$
有一個 $N \times N$ 的白布,有三支顏色分別是紅、黃、藍的滴墨管,在時間 $0$ 的時候,它們會同時在某三個位置滴下墨水,滴下之後墨水會八方位擴散,並且不同顏色會混色(請看題目敘述裡面的圖片),求某個顏色 $X$ 曾出現過的最大面積。
條件限制
- $T$ 筆輸入,$T \leq 5$
- $N \leq 1000$
有一個 $n \times m$ 的迷宮,有些格子是空地,有些是障礙物。有一些格子上一開始有怪物,每過一秒,你可以往上、下、左、右移動一格,且每一隻怪物可能會往它自己的上、下、左、右移動一格,也有可能不會動。你想要從指定的起點走到任意一個迷宮邊界的格子,求一條這樣的路徑,滿足無論怪物怎麼移動,你都絕對不會跟任何怪物同時出現在同一個格子裡。
條件限制
- $n,m \leq 1000$
有 $n$ 個量杯,容量分別為 $m_1,m_2,\dots,m_n$,一開始它們都是空的,你可以做的操作有:
- 把某個量杯裝滿水。
- 把某個量杯的水都倒掉。
- 把一個量杯 $A$ 的水倒到另一個量杯 $B$,直到 $A$ 空了或 $B$ 滿了為止(不能倒到一半)。
求至少要幾步才能讓隨意一個量杯裡的水量恰好是 $t$。
條件限制
- $1 \leq n \leq 5$
- $1 \leq t,m_i \leq 50$