分治法的「分治」指的是「分而治之」（divide and conquer），顧名思義就是把問題分成幾個部分再做。

當要一次做完整個題目不太容易的時候，試著把問題切成一些規模比較小，但形式相同的問題，再各自獨立解決，或許會是一個有效的方法。

$N$ 一定是形如 $2^k$ 的數字，似乎就在暗示我們要把 $N \times N$ 的棋盤分成 4 個 $(N/2) \times (N/2)$ 的區域，要是我們可以把這 4 個 $2^{k-1} \times 2^{k-1}$ 的區域都個別填滿，那全部拼起來就是全部的答案了！不幸的是，要把 4 個區域分別填滿是不可能的，因為除了 $(X,Y)$ 所在的區域以外的 3 個區域，都有 $2^{k-1} \times 2^{k-1}$ 個格子要鋪，而這個數量很顯然不是 $3$ 的倍數，因此我們勢必需要有一些跨越區域的積木。

那問題就麻煩了，要是我們隨便亂放一些跨越區域的積木，讓每個區域的格子數都變成 $3$ 的倍數，也不見得每個區域都鋪得了。我們先來看看一些 $N$ 小的狀況：$N=1$ 的話什麼都不用做。如果 $N=2$，那分出來的 4 個 $1 \times 1$ 區域，有 $(X,Y)$ 的那一個就是只有 $(X,Y)$，不用也不能鋪積木，所以不用理它，而另外 3 個區域就拿一個積木一起鋪起來就解決了。而 $N=4$ 的狀況，分出來的 4 個 $2 \times 2$ 區域裡，有 $(X,Y)$ 的那一個，自己是一個 $2 \times 2$ 的問題，所以就用一個積木把剩下那 3 格鋪起來就好。

不管 $(X,Y)$ 在它那個區域的哪一格，補上一個積木後那個區域當然就是被填滿了。剩下的部分，試一下之後就會發現唯一的填法是這樣：

只有中間那塊紫色積木跨越了不同區域，剩下的積木都在同一個區域裡。要是我們想成是先放下中間那塊積木之後，再去分別填滿 3 個區域的話，就會發現這 3 個區域都變成了「邊長是 2 的冪次、有一格被挖掉」的問題，所以只要用 $2 \times 2$ 的作法就結束了。這樣我們就解決了 $N=4$ 的狀況。

讓 $N$ 再大一點點，現在 $N=8$，分 4 塊後會得到 4 個 $4 \times 4$ 的區域，有 $(X,Y)$ 的那一個自己是 $4 \times 4$ 的問題，可以用剛才的方法解決，然後我們試著跟剛剛做一樣的事：在中間放一個跨越剩下 3 個區域的積木，然後那 3 個區域就各自也是一個 $4 \times 4$ 的問題了！

推廣到更大的 $N$，對於 $N=2^k$，我們的作法就是先分出 4 個 $2^{k-1} \times 2^{k-1}$ 的區域，在中間放一個積木，跨越沒有 $(X,Y)$ 的那 3 個區域，然後遞迴處理 4 個區域。當我們遞迴處理一個區域的時候，那個區域跟本來題目要解決的問題是完全一樣的：邊長是 2 的冪次、有一格被挖掉，等同於我們把一個大的問題變成 4 個比較小的、一樣的問題。當問題變成 $1 \times 1$ 的時候，沒有格子需要鋪，所以就不用繼續遞迴下去。

時間複雜度乍看之下不太好算。$(X,Y)$ 作為問題的輸入，我們不用找它就可以知道它在哪裡了，我們可以 $O(1)$ 得知它在哪個區域、中間的積木要怎麼放、4 個子問題各自的 $(X,Y)$ 在哪裡，所以花費的總時間會是 $O(1)+3 \times (\text{解決 \((N/2) \times (N/2) \) 問題需要的時間)}$，可以想成是每次呼叫這個解決問題的遞迴 function，就會額外花 $O(1)$ 的時間。

• 每次呼叫 function 的 $N \geq 2$ 時，就會多放一個積木，所以除了 $N=1$ 的 function 呼叫之外，總時間和積木數量一樣，都是 $O(N^2)$。
• 呼叫 function 的 $N=1$ 時，注意到會出現 $N=1$ 的呼叫，一定是從一個 $N=2$ 的呼叫來的，而這種呼叫最多 $O(N^2)$ 個、每個會有 3 個 $N=1$ 的子問題，所以 $N=1$ 的呼叫總數是 $O(N^2)$。

因此，總時間複雜度就是 $O(N^2)$。

我們已經見識到了分治法最基本的型態：把問題轉換成一些規模比較小，但是需求跟本來完全一樣的問題。不過，很多時候問題沒有那麼單純，可能不能只是單純地把問題分成一些子問題，然後各自解決、直接拼起來當成大問題的答案，而是要從子問題的答案再多做一些事情，才能得出大問題的答案。

最經典的例子就是合併排序法（mergesort），它是一種排序演算法，目標就是把一個陣列由小到大排序。要是我們直接把陣列切成兩半，兩邊各自排序後，這樣直接拼起來的結果當然不一定是整個陣列排序後應該要有的樣子，所以我們要想辦法從兩半排序好的結果，得出整個陣列排序過的結果。

假設兩邊排序好的陣列分別是 $L$ 跟 $R$，那麼整個陣列裡面最小的數字，當然就是 $L$ 跟 $R$ 第一個數字裡面比較小的那個，把那個數字拔掉以後，$L$ 跟 $R$ 第一個數字比較小的那個就是整個陣列第二小的數字，如此不斷操作，直到把整個排序好的陣列找出來為止，就可以找到整個陣列排序過後的答案了。

// 排序 arr[l], arr[l + 1], ..., arr[r]
void mergesort(int l, int r) {
    if (l >= r) return; // 只有 1 個東西就不必排了
    int mid = (l + r) / 2;
    mergesort(l, mid);
    mergesort(mid + 1, r);
    // 左側是 [l, mid]，右側是 [mid + 1, r]
    // 目前左邊剩下來的第一個元素是 lp，右邊第一個是 rp
    // 目前在找排序完應該要放在 arr[ptr] 的是什麼
    int lp = l, rp = mid + 1, ptr = l;
    while (lp <= mid || rp <= r) { // 還有一側沒有拿完
        // 左側的比較小，rp > r 代表右邊是空的，一樣小的時候優先拿左側
        if (rp > r || (lp <= mid && arr[lp] <= arr[rp])) {
            tmp[ptr] = arr[lp];
            ptr++; lp++;
        }
        else { // 右側的比較小
            tmp[ptr] = arr[rp];
            ptr++; rp++;
        }
    }
    // 把東西從暫存陣列拿回 arr
    for (int i = l; i <= r; i++)
        arr[i] = tmp[i];
}

這樣做的話時間複雜度是什麼呢？我們把遞迴的過程畫出來的話，會像是這樣：

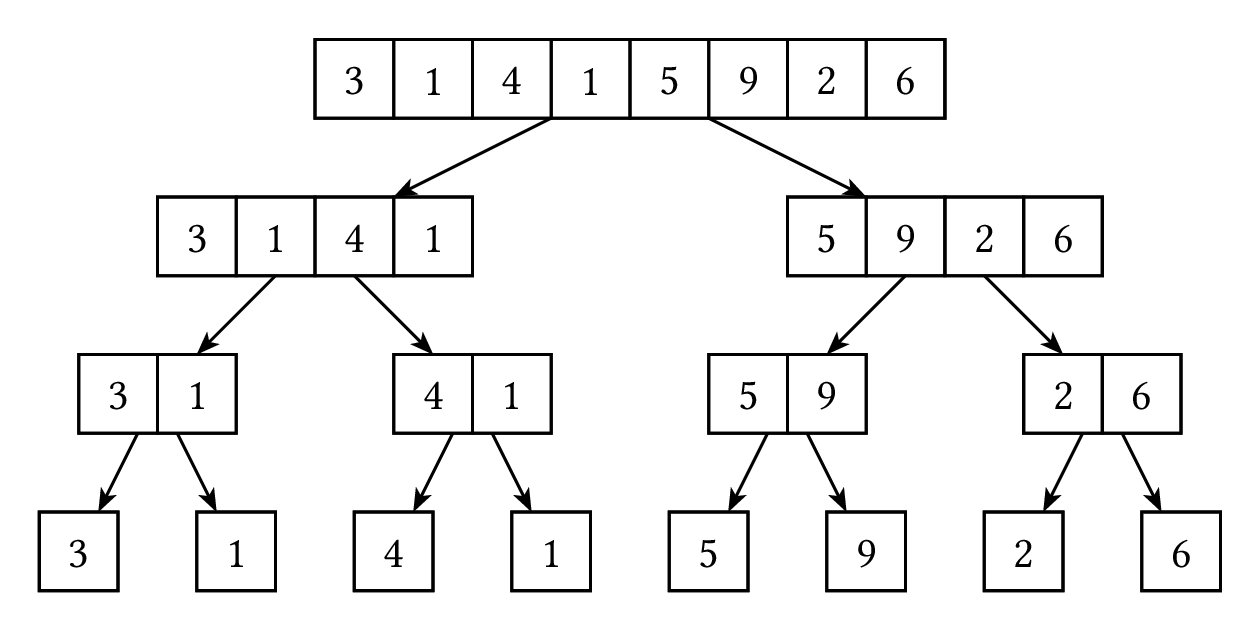
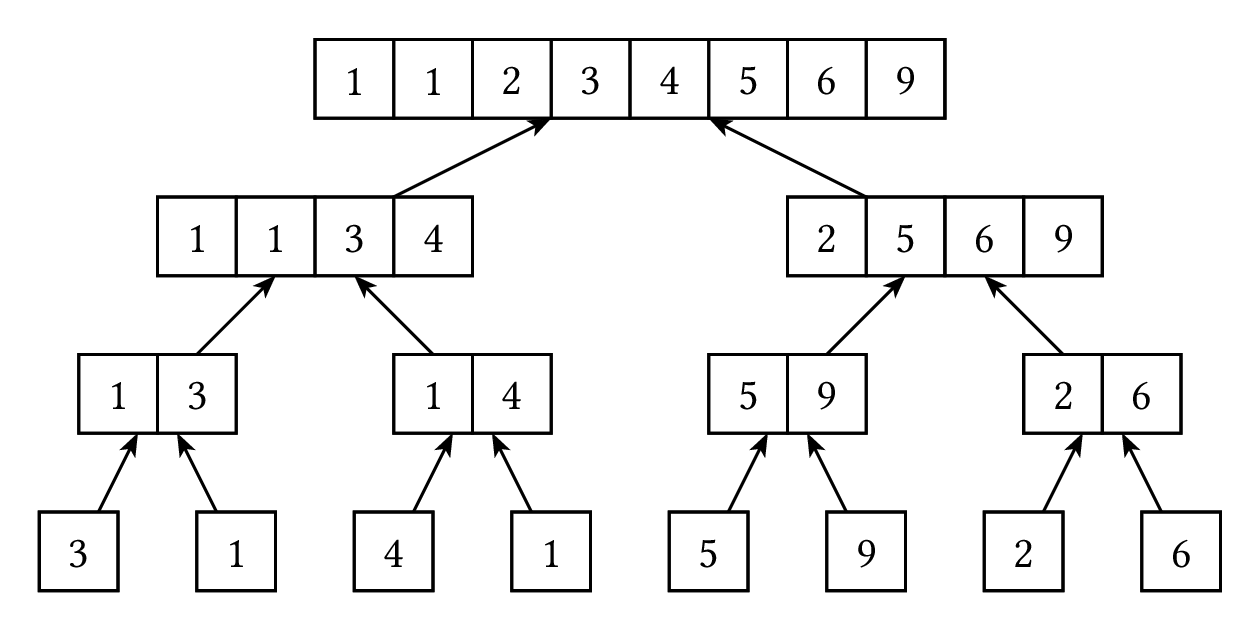
上面那張圖是分割陣列的過程，下面那張圖則是合併回來的過程。當我們合併兩個大小分別為 $a,b$ 的陣列時，我們只會把每個元素各拿出陣列一次，所以時間複雜度是 $O(a+b)$，因此，把一個長度為 $x$ 的陣列排序要花的時間，就是排序兩半的時間再加上 $O(x)$ 的合併時間，所以我們只要算每次呼叫這個排序函數的陣列總長，就是排序要花費的總時間了。

從這兩張圖裡可以看到，分治法的遞迴過程是一層一層的，上面那張圖是往下遞迴、下面那張圖則是遞迴完了 return 回來。畢竟我們是把陣列一直分割，所以本來陣列裡的每個元素自然只會在同一層出現剛好一次，一層的總長度就是 $O(n)$，而因為我們每次都是從中間等分成兩半，可以理解為每次遞迴呼叫的時候，長度就會除以 2，所以層數就是 $O(\log n)$，每一層全部要花 $O(n)$ 的時間，總時間複雜度是 $O(n \log n)$。畫出遞迴過程通常對分析時間很有幫助。

分治法中要求的子問題答案可以不只有題目問的東西！

在基礎演算法 / 枚舉和基礎動態規劃 / 動態規劃的必要元素有提到過別種這題的作法，這題也可以用分治法做，請先遺忘別的作法。

前面的例題中，我們做的事情是「對於子問題找出題目要求的資訊，再得出整個問題的答案」，像是題目要鋪積木我們就在一個小區域鋪積木、題目要排序我們就把半邊的陣列排序，直接在這題這麼做的話，我們按照剛才的想法把陣列切兩半，得出左半邊和右半邊的最大區間和後……就不知道要怎麼辦了，好像沒辦法用這點資訊就找到整個陣列的最大區間和。

在知道左半邊和右半邊的最大區間和後，我們唯一會漏掉的就是「跨越兩半的最大區間和」，也就是我們只要找到跨過中線的最大區間和就好了，這個區間又可以從中線分為左半和右半，左半會緊貼著左側的右界、右半會緊貼著右側的左界，兩半各自越大越好，因此跨越中線的最大區間和，就是左側的最大後綴和，再加上右側的最大前綴和。

如果目前處理的區間長度是 $O(x)$，遞迴處理兩側之後，兩側的後綴和跟前綴和需要 $O(x)$ 的時間計算，因此總時間複雜度和合併排序法一樣，都是 $O(n \log n)$。這樣聽起來很遜，明明就有 $O(n)$ 的作法，這個方法還比較不好寫，分治法有辦法把這個問題做到 $O(n)$ 嗎？

我們剛才做的事情是「兩邊做完之後再處理跨中間的狀況」，但我們處理跨中間的狀況，實際上是問了兩個只在一側的問題：左側的最大後綴和跟右側的最大前綴和，如果我們改成在遞迴呼叫解決問題的函數時，要求它一併告訴我們自己的最大前綴和跟後綴和，那流程會是這樣：

• 如果區間大小是 1，那麼最大前綴和、最大後綴和、最大區間和都是區間裡面那個唯一的數字。
• 否則，把區間分成兩半遞迴處理，然後回傳：
  • 整個區間的最大區間和：左右側最大區間和以及左側最大後綴和加上右側最大前綴和的最大值。
  • 整個區間的最大前綴和：左側最大前綴和以及左側總和加上右側最大前綴和的較大值。
  • 整個區間的最大後綴和：右側最大後綴和以及右側總和加上左側最大後綴和的較大值。

把這些合併兩側答案的方法都列出來後，會發現還需要區間總和才能知道新的最大前後綴和，當然不能暴力算一遍，不然時間複雜度不會變好，我們可以再讓每個子問題也回傳自己的區間總和，長度為 1 的區間總和也是裡面那個唯一的數字，而合併兩側區間就是直接把兩側總和相加。

這樣做的話，合併兩側區間、計算整個區間的答案需要花費的時間只有 $O(1)$，所以花費的總時間就是我們呼叫解決問題 function 的總次數，剛才說到遞迴過程有 $O(\log n)$ 層，因為每一次呼叫都最多只會分出兩個呼叫，第一層只有 1 次呼叫，因此第 2 層最多只有 2 次呼叫、第 4 層最多只有 4 次呼叫、……，總呼叫次數大概會是 $1+2+4+8+\dots+2^{\log n} \leq 2n$，總時間複雜度就是 $O(n)$ 了！

盡可能把能讓子問題處理的事情丟包給子問題負責，有時就會像這樣有降低時間複雜度的效果。有些更複雜的問題裡面，計算跨越中間的答案時需要知道的資訊，也不一定像最大前後綴總和一樣可以在 $O(x)$ 這種還算快的時間算完，這時適當地把任務丟包下去就會大有助益。

直接利用我們一直使用的分治法想法：把要處理的陣列切一半，計算左邊的逆序數對數量、右邊的逆序數對數量，然後再計算跨越兩側的逆序數對數量，全部加起來就是整個陣列裡的逆序數對數量。

要怎麼計算跨越兩側的逆序數對數量呢？跨越兩側就是要 $i$ 在左邊、$j$ 在右邊，然後 $s_i > s_j$，如果我們對於每個左邊的 $i$，去數有幾個右邊 $j$ 跟它形成逆序數對，那這個數量就是右邊有幾個 $j$ 滿足 $s_i > s_j$。陣列長度是 $x$ 時直接暴力做的複雜度是 $O(\frac x2 \times \frac x2)=O(x^2)$ 當然很不好，如果我們先把右邊排序好的話，那每個左側的 $i$ 都可以用 $O(\log \frac x2)=O(\log x)$ 的時間二分搜問出 $j$ 的數量，這樣做的時間複雜度是 $O(x \log x)$，這樣多乘一個 $\log x \leq \log n$ 感覺總時間就會也多乘上 $O(\log n)$，會花上 $O(n \log^2 n)$ 的時間。（雖然我們直接把 $\log x$ 灌水成 $\log n$，其實可以證明 $O(n \log^2 n)$ 是緊的時間複雜度！）

注意到「把右側排序」是一個只跟右側有關的問題，所以其實可以直接丟包給子問題處理，因此我們為每次呼叫都多指派一個任務：要把陣列排序好，一邊做合併排序就可以做到了。然而要是對每個左側的 $i$ 都還是用二分搜去找右側跟它形成逆序數對的 $j$ 數量的話，還是得花 $O(x \log x)$ 的時間，別忘了我們遞迴下去的時候順便把左邊也排序好了，所以問題會是「在排序好的陣列 $L,R$ 中，對 $L$ 裡的每個元素，找出 $R$ 裡面有幾個比它小的」，對於 $L$ 裡某個元素 $L_i$，$R$ 裡面比它還小的 $R_j$，一定是 $R$ 的一個前綴，找到最後一個 $<L_i$ 的 $R_j$ 就知道是有 $j$ 個了，這個問題可以用雙指針在 $O(x)$ 的時間解決。

別急著寫雙指針，因為寫出來會跟合併排序中的合併一樣，其實比 $L_i$ 小的 $R_j$ 數量，根本就是在合併過程中，$L_i$ 被拿出來時，$R_j$ 已經被拿走的數量嘛，因此只要稍微修改合併排序的過程，就可以算出逆序數對數量了。

#include <bits/stdc++.h>
using namespace std;

const int MAXN = 100000;

int arr[MAXN];

int tmp[MAXN];
long long ans = 0;
void solve(int l, int r) {
    if (l >= r) return;
    int mid = (l + r) / 2;
    solve(l, mid);
    solve(mid + 1, r);
    int lp = l, rp = mid + 1, ptr = l;
    while (lp <= mid || rp <= r) {
        // 注意 tie-break！
        if (rp > r || (lp <= mid && arr[lp] <= arr[rp])) {
            ans += rp - (mid + 1); // 加這個
            tmp[ptr] = arr[lp];
            ptr++; lp++;
        }
        else {
            tmp[ptr] = arr[rp];
            ptr++; rp++;
        }
    }
    for (int i = l; i <= r; i++)
        arr[i] = tmp[i];
}

int main() {
    
    int n;
    int t = 0;
    while (cin >> n) {
        if (n == 0) break;
        ans = 0; // 開全域變數要記得初始化
        t++;
        for (int i = 0; i < n; i++) cin >> arr[i];
        solve(0, n - 1);
        cout << "Case #" << t << ": " << ans << "\n";
    }
    
}

也就比合併排序多一行，時間複雜度一樣是 $O(n \log n)$。

在最大區間和以及合併排序中，我們都是把要處理的區間原封不動分兩半，當成兩個子問題遞迴處理，再從兩個子問題的答案（包含另外丟包的任務）得出要處理的區間的答案。在分子問題的時候其實不一定要原封不動地分，例如做王老先生的時候我們是先放一個積木、稍微改變了子問題，再遞迴下去處理，當然分子問題之前也可以把陣列的長相改得面目全非。

快速排序法（quicksort）是另一種排序法，當然目標也是把陣列排序。合併排序的想法是先分兩半、各自排序，然後合併，而快速排序的想法是把小的數字放到一邊、大的數字放到一邊，兩邊各自排序後，整個陣列就會自然排序好了。然而，要想把數字按照大小分成兩堆其實沒那麼容易，前面合併排序的時間複雜度可以是 $O(n \log n)$，是因為我們每次都把區間等分成差不多兩半（奇數的時候大小會差 1），讓遞迴層數是 $O(\log n)$，如果我們要在不排序的前提下，將數字按大小分兩堆、且兩堆差不多大，那就得找到中位數，這並不是一件輕鬆的事情，而如果隨便挑一個數字的分界線，那要是每次都不幸地選到最小的數字，本來區間長度是 $x$ 的話，左半就會只有 $1$、右半長度是 $x-1$，時間複雜度就會變成淒慘的 $n+(n-1)+\dots+1=O(n^2)$！

要想讓花費的時間盡量少，每次就得盡量挑到靠近中位數的分界線，一個方法是直接隨機選一個區間中的數字作為分界，可以感性認為取到靠近中間的數字當分界的機率很高，所以遞迴層數的期望值也是 $O(n \log n)$。這個分析方法非常不嚴謹，不過這是對的，對細節有興趣的讀者可以點開下面的證明。

看了這麼多例子，我們已經知道分治法的基本精神了：

• 把問題分成一些子問題。
• 遞迴地解決子問題。
• 用子問題的答案拼湊出整個問題的答案。

在設計分治演算法的時候，可以先明確規定好一個問題要長什麼樣子、做完之後應該要給出什麼答案，通常「問題的樣子」就和題目給的問題長得一樣，不過做完問題之後我們的函式要回傳的答案除了本來題目要求的答案之外，可以再包含更多資訊，像是在算逆序數對時，我們的解決問題函式不僅回傳了逆序數對數量，還得要把那個區間排序好。先規定好這些「任務」之後，就可以先假裝遞迴解決子問題後，我們要求的任務一定會被完成，然後再去想要怎麼從子問題完成的任務結果，來完成大問題的任務。要是發現資訊不夠多，除了自己算出來之外，也可以把一些事情加入任務裡，作為任務的一部分，然後丟包給子問題做。

看完上面的例子，讀者有可能不會意識到分治法的重要性，畢竟剛才的例子幾乎都有別的作法的替代品：

• 合併排序、快速排序都是在排序，只要呼叫 std::sort 就解決了，根本就不用自己分治嘛。
• 最大區間和有好幾種時間複雜度也是 $O(n)$，而且還好寫很多的作法，那麼麻煩幹嘛？
• 如果讀者聽說過像是 BIT、線段樹這類的資料結構，這些資料結構支援「修改一個陣列的一個數值、查詢區間總和」，可能會發現要算逆序數對，只要從左邊看到右邊，用資料結構維護「每種數字出現的次數」，看到一個數字時，只要查比它大的數字出現過幾次、加到總答案去，就可以得到逆序數對數量了。所以，其實也不一定需要分治。

好像只有王老先生那種分治構造題才不太好避免分治。的確，很多可以用分治法解決的問題，都有「表面上不是分治」的替代作法，為什麼是說「表面上」呢？因為分治法其實是演算法的設計精神，很多時候會被隱藏在其他有名字的東西裡頭，像是線段樹這個資料結構，其實完全就是基於分治的理念，如果讀者不知道什麼是線段樹，還有一些更簡單的例子：

• 二分搜尋法（請看基礎演算法 / 搜尋）其實也是分治！只是我們把搜尋範圍分成兩半以後，有一半不用做，只要做有答案的那一半就好。
• 快速冪（請看基礎數學 / 常用數學演算法）其實也是分治！$a^{2k}$ 會被分成 $a^k \times a^k$ 兩個子問題的答案相乘，兩個子問題一模一樣，所以只做一次就好。

那最大區間和有別的作法要怎麼解釋？DP 或前綴和的作法總不是分治了吧！確實其他作法就比較沒有分治的成分在，但分治法用在這個問題可是很厲害的，像是下面習題放的「最大連續和？」，問的是多次查詢一個指定區間之中，最大的區間和，這一類的問題最常用的方法就是使用分治法（或基於分治法的資料結構，其實這題更常會被用線段樹做掉，但其實是可以純使用分治法的）了。

現階段讀者也有可能真的還感受不到分治法的重要性，但可以先把「很多演算法背後都是分治法」這件事記在心裡，往後學到更多技巧時，有時就會發現背後的概念就只是分治法，熟練分治法的話也可以更快速地學會這些技巧、學習那些技巧也能幫助理解分治法。