例題

列舉八皇后問題所有解

Source:ZeroJudge i644

西洋棋這個遊戲是在一個 $8 \times 8$ 的棋盤上進行的，我們定義棋盤的左上角那一格是 $(1,1)$、第 $r$ 列（row）第 $c$ 行（column）的格子是 $(r,c)$。在西洋棋中，一個皇后可以吃到跟它在同一行、同一列或同一條斜線上其他棋子，現在有一個空的棋盤，請你在棋盤上放置恰好 $8$ 個皇后，使得它們都不能吃到對方。

請輸出所有可能的放法，一個放法以第 8 個數字表示，其中第 $i$ 個數字代表第 $i$ 橫列（row）上的棋子要放在哪一個直行（column），按照字典序輸出。也就是說，如果有兩種不一樣的放法，在它們第一個放在不同直行的橫列上，放得比較左邊的放法要優先被輸出。

既然題目都要我們列出所有放法了，那想必就是很暴力地枚舉出全部的可能性就結束了，不過要怎麼列出全部的可能性呢？試想一下如果我們試圖自己在紙上畫出一個解，方法不外乎就是先隨便放一個、再找一個看似合理的地方放第二個，不斷找一個「感覺合理的地方」放，要是在放滿 8 個之前，就已經找不到合理的地方放了，那就把上一個放的棋子擦掉，換一個地方放。

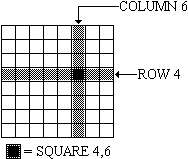
我們用個小一點的棋盤來舉例，假設我們現在要在 $4 \times 4$ 棋盤上放 4 個皇后：

• 一開始我們先選一格放，假設就是左上角那格，然後我們把會被它吃到的格子先標記成不能放東西，得到下圖的 (1)。
• 再選一個可以放的格子，不過如果我們放成 (2) 那個樣子，會發現剩下能放東西的格子只剩一格。
• 我們就直接回到上一步（回到 (1) 的狀態）、換一個地方放，變成 (3) 那樣。
• 無論下一個棋子放在哪裡，最後一個棋子都不會有地方可以放。
• 每一橫列總得要放一個棋子，但我們已經在放下左上角那個棋子以後，試過第二列的所有放法了，因此我們勢必得重放第一列的棋子。所以我們把第一列棋子往右放一格，得到 (5)。

接下來順順的放完就成功了！

別忘了本來要做的問題是「列出所有可能」，所以就是我們放了一個棋子後，試完了所有可能性，就把這個棋子換下一個地方放繼續試。

要用程式做的話，我們先利用剛剛提到的「每一橫列要放恰好一個棋子」，在放第 $i$ 個棋子的時候，我們就一一嘗試第 $i$ 橫列的「不會被已放置棋子吃到」的格子，放下這一列的棋子後，再去放下一個棋子。發現了嗎？這個過程其實就是遞迴！

#include <bits/stdc++.h>
using namespace std;

int ans[9];
int cnt = 0;
// ans[i] = 第 i 列的棋子放在哪裡
// cnt = 已經找到了幾個解
void solve(int x) { // 現在要放第 x 列的棋子
    if (x == 9) { // 找到一個解了
        cnt++;
        cout << cnt << ": ";
        for (int i = 1; i <= 8; i++) cout << ans[i];
        cout << "\n";
        return;
    }
    // 放在 (x, i)
    for (int i = 1; i <= 8; i++) {
        bool ok = true;
        for (int j = 1; j < x; j++) {
            // 檢查 (j, ans[j]) 的那個棋子會不會吃到這一格
            if (ans[j] == i) ok = false; // 同個 column
            if (ans[j] + j == i + x) ok = false; // 同個左下右上斜線
            if (ans[j] - j == i - x) ok = false; // 同個左上右下斜線
        }
        if (!ok) continue;
        ans[x] = i;
        solve(x + 1); // 繼續做下一列
    }
}

int main() {
    solve(1);
}

檢查要放的位置 $(x,i)$ 究竟能不能放（會不會被之前放的棋子吃到）可以做得更快一些，像是用幾個陣列來存每一個直行、斜線有沒有放過東西，這部分的細節就留給讀者自己嘗試了。

在剛剛的例題裡，讀者可能有發現，由於每一直行、橫列都得放恰一個棋子，因此我們把每一橫列棋子所在的直行行號列出來，會是一個 $1 \sim 8$ 的排列，讀者可能會想到要用基礎演算法 / 枚舉中提過的枚舉排列，事實上拿掉上面的「檢查有沒有棋子在同一個斜線上」，那就是在枚舉排列了，所以也可以想成是我們在枚舉排列的過程中，把一些「不可能成為我們要求的解」的排列直接丟掉了，跟枚舉排列最後再檢查相比，多省去了一些不必要的枚舉。

換一個方式說，就是我們在尋找解的過程中，可能到一半就發現我們走在一條錯誤的道路上，繼續走下去怎麼找都不會找到我們想要的答案，此時我們可以直接放棄這一條路，這個動作就稱為「剪枝」。

我們再看一個例題：

很直覺地可以直接用枚舉裡面枚舉子集的方法，枚舉所有子集並檢查總和，不過這樣就會枚舉到全部的集合，如果我們用像剛剛一樣的思路自己用遞迴枚舉，並且過程中總和太大就直接剪枝，這樣一來我們枚舉的集合數量就剛好會是答案大小了。

#include <bits/stdc++.h>
using namespace std;

const int MAXN = 100;
int n;
long long K;
int a[MAXN];
bool chosen[MAXN + 1];
// chosen[i] = 第 i 個數字要不要選

// 現在要決定第 id 個數字要不要選
// 之前選過的數字總和是 sum
void dfs(int id, long long sum) {
    if (id == n + 1) {
        for (int i = 1; i <= n; i++)
            if (chosen[i]) cout << i << " ";
        cout << "\n"; // 空的會輸出空行
        return;
    }
    // 不要選 id
    chosen[id] = 0;
    dfs(id + 1, sum);
    // 要選 id，並且遞迴之前先檢查總和會不會超過
    chosen[id] = 1;
    if (sum + a[id] <= K) dfs(id + 1, sum + a[id]);
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(0);
    
    cin >> n >> K;
    for (int i = 1; i <= n; i++) cin >> a[i];
    dfs(1, 0);

}

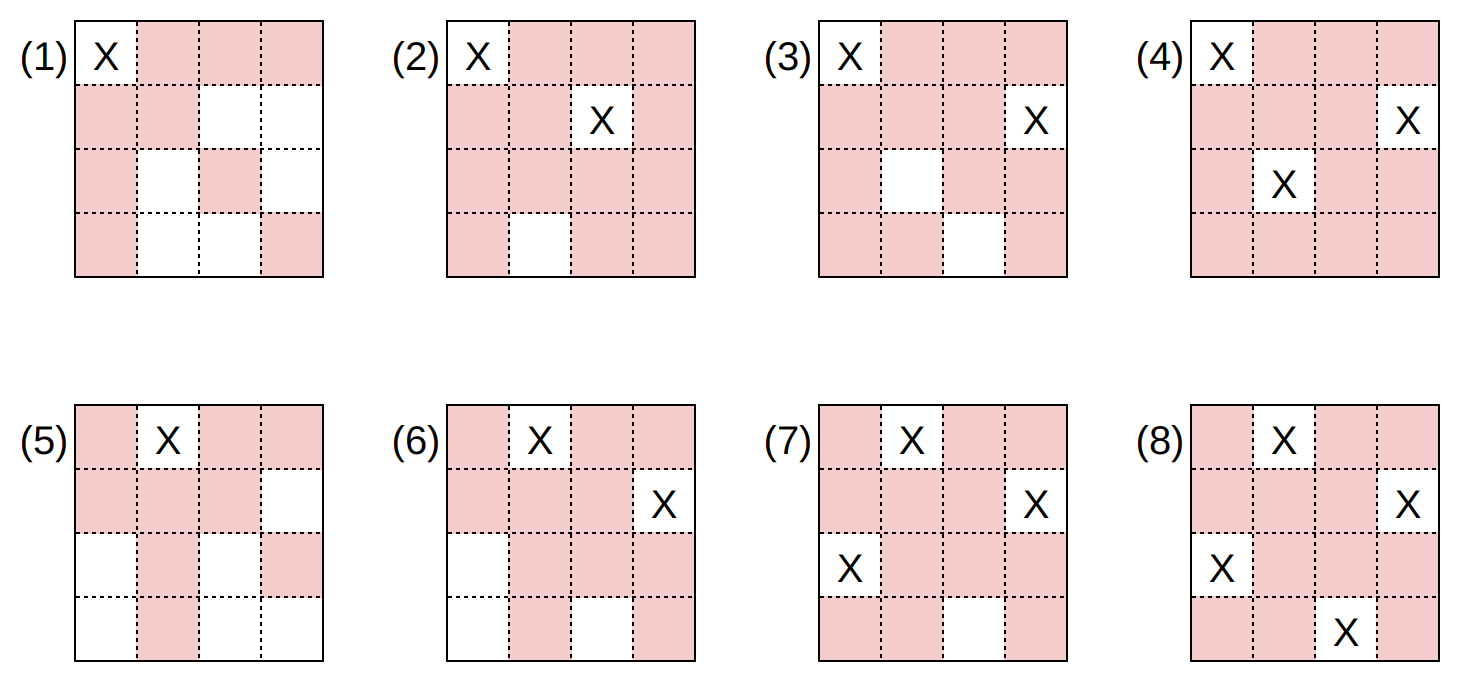
純手工要枚舉所有集合的話，可能會想要畫一個樹狀圖，遞迴的過程就很像是這樣做。像是假設 $n=4,k=10,a=[1,4,6,8]$：

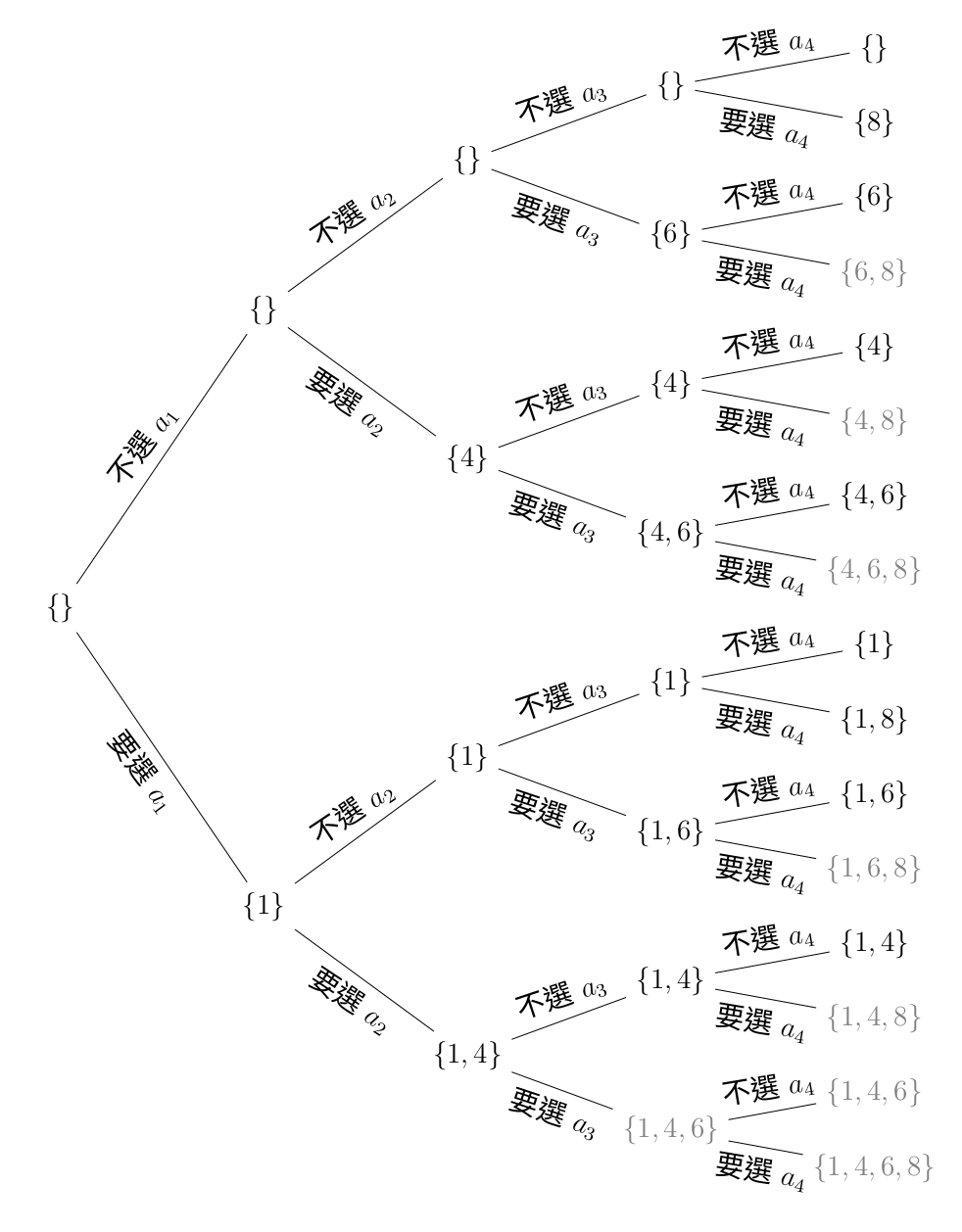
那些灰色的集合就是總和超過 $k=10$ 的集合，因為我們在遞迴之前就會先檢查總和有沒有超過 $k$，所以上面的程式碼是不會枚舉出灰色的集合的。

有的時候，剪枝過的枚舉方式會有點難計算時間複雜度，像是前面的八皇后，因為有可能放了好幾個棋子後才發現這條路行不通，而且最後放的幾個棋子全部都不該那樣放，我們可能浪費非常多時間在枚舉不會有答案的放法，就連用答案數量來表示花費時間都不太容易。不過，在這個例子就明顯許多：假設答案有 $x$ 個，那樹狀圖上走到底也只有 $x$ 個集合，枚舉出這些集合的路上我們會走 $n$ 步，所以時間複雜度就是 $O(nx)$。想想看樹狀圖的樣子通常可以幫助分析花費時間。

嗯？你問 function 名稱 dfs 是什麼意思？

這種枚舉方式的核心精神就是，我們先「做出一個決定」，像是一個棋子要放在哪一格、或是某一個數字要不要選，然後就朝著做出這個決定之後的未來前進，直到我們探索完「做出這個決定以後」的所有可能性以後，我們把這個決定反悔、改做另一個決定，以此來找出所有「做決定」的可能性。這種「一旦決定以後就去把所有接下來的可能性找完」的搜尋方法，稱為深度優先搜尋（Depth-First Search），可以想成「深度優先」的意思是我們會優先往上面那種樹狀圖的深處走。

剛才八皇后那一題有要求「要按照字典序輸出答案」，因為我們在每個橫列都是「先試試看把棋子放在第一格、再試第二格、……」，所以我們發現答案的順序會很自然地滿足答案要求。至於在枚舉總和有上限的子集那題，因為答案是可以用任意順序輸出的，所以我們怎麼找都可以，但要是多加上一個限制「要按照字典序輸出」的話，剛才的寫法就行不通了！像是剛才舉的 $a=[1,4,6,8]$ 的例子，上面程式碼會輸出：

(這是一個空行)
4 
3 
2 
2 3 
1 
1 4 
1 3 
1 2 

但照字典序的話應該要是：

(這是一個空行)
1 
1 2 
1 3 
1 4 
2 
3 
4 
2 3 

會不會原因是我們先枚舉不選的狀況、再枚舉要選的狀況呢？事情沒那麼簡單，要是直接把順序對調，會得到的輸出是（其實就是剛才的輸出直接反過來）：

1 2 
1 3 
1 4 
1 
2 3 
2 
3 
4 
(這是一個空行)

當然有一個非常無腦的方法是先把所有答案存下來，排序後再輸出，但這麼做的缺點很多，除了寫起來麻煩以外，還要多花排序的時間以及存下所有答案的空間（本來的空間複雜度可是非常好的 $O(n)$！），要是可以直接用要求的順序枚舉出答案，那當然再好不過。這題就留給讀者想想要怎麼在不先存下來再排序的情況下，用正確的順序輸出答案。

我們就直接……暴力找出所有的走法？

#include <bits/stdc++.h>
using namespace std;

const int MAXN = 1000;
int n;
string maze[MAXN + 2];

using pii = pair<int, int>;
pii dir[4] = {pii(-1, 0), pii(1, 0), pii(0, -1), pii(0, 1)};
string dir_char = "UDLR";
string cur; // 表示目前走法的字串
void dfs(int x, int y) {
    if (x == n && y == n) {
        cout << cur << "\n";
        exit(0); // 直接結束程式
    }
    for (auto [dx, dy] : dir) {
        int nx = x + dx, ny = y + dy;
        // 不要走進障礙物
        if (maze[nx][ny] == '#') continue;
        cur += dir_char[i];
        dfs(nx, ny);
        cur.pop_back(); // 要記得拔掉
    }
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(0);
    
    cin >> n;
    // 直接在外面多加一圈障礙物防止走出去
    for (int i = 1; i <= n; i++) {
        cin >> maze[i];
        maze[i] = '#' + maze[i] + '#';
    }
    maze[0] = maze[n + 1] = string(n + 2, '#');
    dfs(1, 1);

}

光是 $n=2$、沒有障礙物都走不出來！這是因為我們會先往下走、再往上走、再往下走、再往上走……如此無限重複，其實我們走的路線沒有必要繞圈圈，也就是經過重複的地方嘛，所以可以記錄一下每個格子是不是在目前路線上，不要走到已經在路上的格子：

// vst[x][y]= (x,y) 是不是在路線上
bool vst[MAXN + 2][MAXN + 2];
void dfs(int x, int y) {
    vst[x][y] = true;
    if (x == n && y == n) {
        cout << cur << "\n";
        exit(0); // 直接結束程式
    }
    for (auto [dx, dy] : dir) {
        int nx = x + dx, ny = y + dy;
        // 不要走進障礙物
        if (maze[nx][ny] == '#') continue;
        // 不要走到已經在路線上的格子
        if (vst[nx][ny]) continue;
        cur += dir_char[i];
        dfs(nx, ny);
        cur.pop_back(); // 要記得拔掉
    }
    vst[x][y] = false; // 要記得還原
}

然而，在這筆測資：

10
..........
.########.
........#.
........#.
........#.
........#.
........#.
........#.
........#.
........#.

會跑超級久！雖然我們一眼就可以看出唯一的走法是走進右邊那條狹窄的走道，但我們的程式會先走進左下方那個大塊區域，然後試過所有在那個區域裡面的走法，這會花上非常多的時間。其實，我們並不需要知道走到一個格子的所有走法，而是只要知道其中一種就好了，所以我們其實不需要把 vst[nx][ny] 還原成 false，只要把上面程式碼裡的第 19 行拔掉，就能成功輸出答案了！

作法變成這樣後，與其想成我們是在「搜尋走法」，不如說我們其實是在找「所有走得到的地方」，要是我們不要管走到 $(n,n)$ 了沒，也就是把上面程式碼的 5 到 8 行也拔掉，那呼叫 dfs(1, 1) 之後，vst[x][y] 就代表從 $(1,1)$ 能不能走到 $(x,y)$，所以想成我們是在搜尋能夠走到的格子還比較直接一點。反正既然我們確定了一個格子可以被走到，當然也就代表我們知道有一條走到那裡的路徑了，DFS 的遞迴過程還會順便隨時幫我們維護好目前走到的地方的路徑。

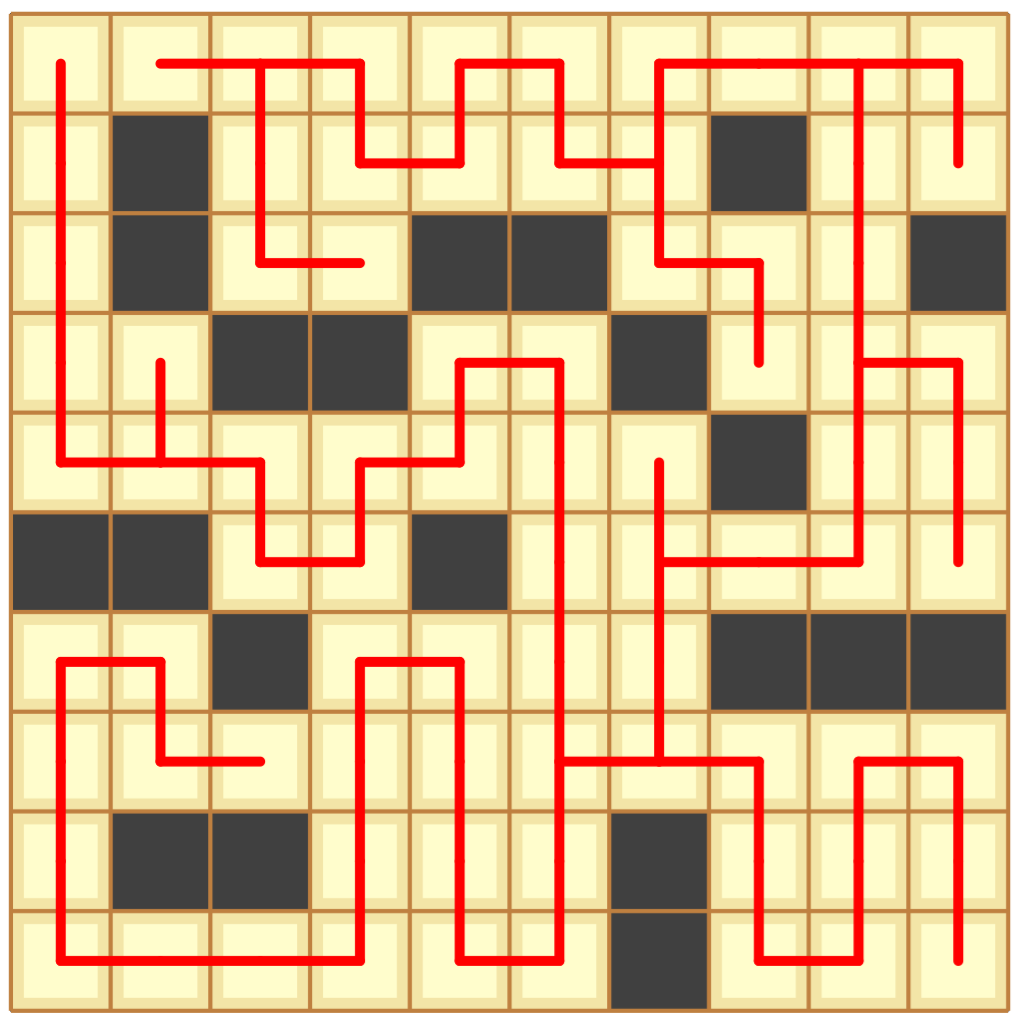
這裡放一個比較複雜的迷宮的例子，讓讀者能更好感受一下 DFS 的過程，紅色線條是從左上角開始走，用上面的寫法 DFS 走遍所有格子會走的路線：

既然剛剛都說 DFS 的過程可以想像成是在畫一張樹狀圖，那我們何不真的對一棵樹 DFS？其實在基礎資料結構 / 二元樹就有做過這件事了，就是這段程式碼：

void travel(node *x) {
    if (!x)  return;
    travel(x->lson);
    printf("%d ",x->val);
    travel(x->rson);
}

那時我們用這個 function 來由小到大印出一棵二元搜尋樹中所有的元素，也就是中序遍歷。

當我們對一個二元樹上的節點 x 呼叫 travel(x) 時，這個 function 就會去走遍它的所有子孫，走的順序是先去走它的左小孩，把左子樹走完後，才會回來、執行第 4 行的 printf、再走去右小孩，右子樹整個走完後再回來，然後結束這個 function。這個過程就是「還可以往下走就先把子孫都走完」，正好就是我們剛剛說的「優先往深處走」。而會先把所有子孫走完的特性，也是為什麼這個 function 會輸出中序遍歷的原因，呼叫 travel(x->lson) 就會把左子樹（比較小的元素）都先輸出、輸出自己之後再呼叫 travel(x->rson) 去輸出右子樹（比較大的元素），合起來就是我們要的中序遍歷。

看了這麼多例子之後，我們統整一下 DFS 的流程：DFS 的實作往往是寫成一個遞迴 function 的形式，在遞迴的過程中，我們會需要知道我們現在枚舉的「狀態」，例如八皇后問題中目前的盤面長什麼樣子、我們放好了幾個橫列就是目前枚舉的狀態，狀態可以寫在 function 的參數，也可以存在全域，像是我們剛才就把「目前盤面的樣子」（ans 陣列）放在全域、「放好了幾個橫列」（參數 x，代表接下來要放的那個橫列）放在 function 參數。在 function 的過程中，就是要枚舉下一步的操作是什麼，計算出對應的狀態改變後，遞迴呼叫 function，呼叫完後要視需要還原剛剛被修改過的狀態。

DFS 可以幫我們以很直觀、像是我們在畫樹狀圖的方式枚舉我們想要的東西。與其說是在枚舉，將 DFS 用「搜尋」的角度理解會更準確一點，使用 DFS 的情境並不只有在我們想要枚舉東西時，像是走迷宮，比起枚舉，我們更像是在尋找所有可以走到的地方，而枚舉物件也可以想成我們是在搜尋所有我們想要枚舉的物件。DFS 除了是一種搜尋的方式之外，「優先往深處走」的特性，有時也可以幫我們達到特殊的目的，中序遍歷就是一個例子，將來我們還會發掘更多 DFS 的特殊用途。

習題

數獨

Source:NEOJ 62

在數獨遊戲中，遊戲給你一個 $9\times 9$ 的方陣，其中還可以分成 $9$ 個 $3\times 3$ 的子方陣。例如：

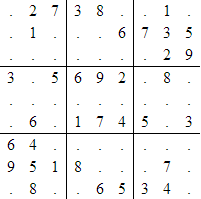
數獨的遊戲規則是這樣的，最後完成數獨的時候，每個格子都必須填上 $1\sim 9$ 其中一個數字，並且在每一行、每一列、每一個子方陣中，都不能有重複的數字。

現在給你一個 $9\times 9$ 的方陣，上面有一些格子已經寫上數字了，你的任務是完成這個數獨。

條件限制

• 每筆測試資料未填上數字的格子數保證不超過 $15$ 個
• 單一測資檔不超過十筆測試資料