假設一位老師要發考卷給班上 $5$ 位學生,反正人也沒很多,每張考卷拿起來再直接找到對應的學生給他就好。
不過如果我們事先排好考卷的順序呢?這樣這位老師只要走過一圈教室就可以把考卷發完了,也不會發生他要反覆從教室一端跑到另一端的狀況。
這樣到底省下了多少時間?我們就假設 $5$ 位學生的座位大概也不會坐太遠,可能最遠也只要花費 $3$ 秒的時間就可以自由的在任兩個學生之間來回。所以最慘就花個 $5\times 3=15$ 秒吧。
如果走過一圈教室也差不多要花 $5$ 秒,照這樣看來,先排好考卷頂多只幫助我們省下 $10$ 秒的時間。好像沒有很多嘛。
但要是學生變成十倍,也就是 $50$ 位呢?這時候在兩個學生之間來回可能就得花費 $30$ 秒,$50$ 位學生更是會讓總花費時間變成 $1500$ 秒!這時,因為走過一圈教室也許只要花 $50$ 秒,所以事先排好考卷的優勢便開始出現了。
更進一步的,如果學生變成 $500$ 位呢?$5000$ 位呢?你能想像這個差距嗎?
在寫程式的世界中,我們常常要面對的就是這種「比平常還要大非常多」的測試資料,很可能動不動就是 $5000$ 行字串、$10^5$ 個數字。想當然的,資料量變多,程式一定會變慢,而所謂的效率,就是能穩定的在數字變大時,還可以控制「程式變慢的幅度」,使得程式雖然變慢了,也不至於太誇張。這才是我們所要追求的「效率」。
我們知道,程式競賽中的題目都有著所謂的「時限」,而判斷自己的演算法在寫成程式後能不能在規定的時限內執行完畢,就得來分析他的效率了。就好比我們寫出了下面這段程式碼:
void bubble_sort(int arr[], int n) {
for (int i = 0; i < n - 1; ++i)
for (int j = 0; j < n - i - 1; ++j)
if (arr[j] > arr[j + 1]) {
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
}
}
那當 $n=10$ 時,他能在一秒內跑完嗎?$n=1000$ 可以嗎?$n=10^5$ 呢?
如果盲目的將程式寫完後就傳上 Online Judge 等待結果,可想而知的就是會時常因為獲得 TLE 而落後其他對自己程式的效率夠清楚的選手。更可怕的是,如果我們設計好的演算法其實不管怎麼樣都無法被寫成一個能在時限內跑完的程式的話,還一無所知的浪費大把時間下去寫,不就白忙一場了嗎?
也因此,提前想清楚自己演算法的效率便成為一個非常重要的事項。
如果我們仔細一行一行計算上面程式所需要花費的「步驟數量」的話,似乎可以這樣條列:
void bubble_sort(int arr[], int n) { // arr: 要排序的陣列,n: 陣列大小
for (int i = 0; i < n - 1; ++i) // n 次運算
for (int j = 0; j < n - i - 1; ++j) // (n - 1) + (n - 2) + ... + 1 = n * (n - 1) / 2 次運算
if (arr[j] > arr[j + 1]) { // n * (n - 1) / 2 次運算
int tmp = arr[j]; // 至多 n * (n - 1) / 2 次運算
arr[j] = arr[j + 1]; // 至多 n * (n - 1) / 2 次運算
arr[j + 1] = tmp; // 至多 n * (n - 1) / 2 次運算
}
}
也因此,可以計算出這個程式需要執行的步驟數量至多為
$$ n + 5 \times \frac{n(n-1)}{2} = \frac{5}{2} n^2 - \frac{3}{2} n$$
在算出步驟數量後,我們就可以去預估程式的執行時間了。因此當 $n=1000$ 時,這個程式至多需要跑 $2.5\times 1000\times 1000-1.5\times 1000=2498500$ 步;而當 $n=10^5$ 時就是 $24999850000$ 步。
等等……算出步驟量然後呢?到底能不能跑進一秒啊?
在現代的程式競賽中,我們會有一些簡單的共識:電腦一秒鐘大約可以跑 $10^9$ 次基礎運算。所謂的基礎運算,就是泛指 C++ 中基本的五則運算(+ - * / %)、變數賦值、陣列存取、條件判斷(< == >)等。
也因此,$n=1000$ 的情況下只需要不用 $0.003$ 秒就可以跑完了,但 $n=10^5$ 時可就要跑大約 $25$ 秒!
讀者讀到這裡可能開始起疑了:怎麼可能每次我分析效率都要這麼麻煩的算式子?
沒錯,我們在設計演算法時,是不會真的把程式先寫出來再一行一行計算的,在講究速度的比賽中,哪有閒功夫做這些瑣碎的麻煩事呢?
為了簡單描述演算法的效率,我們會採用「時間複雜度」這個概念。例如上述的程式,我們會說「他的時間複雜度是 $O(n^2)$」。就讓我們先認識一下這個符號:
$O$ 這個符號讀做 Big-O,表示一個函數成長趨勢的上限。為了表示上限,我們會無視係數、並捨棄那些成長趨勢較緩慢的項。
例如當 $T(n) = \frac{5}{2} n^2 - \frac{3}{2} n$ 時:
- 我們可以丟棄係數 $\frac{5}{2}$ 和 $\frac{3}{2}$ 得到 $n^2 - n$
- 再丟棄成長趨勢比較緩慢的 $n$
就可以直接說 $T(n)$ 是 $O(n^2)$。
省略了這麼多東西有什麼好處呢?我們重新將 $n=1000$ 和 $n=10^5$ 代入 $n^2$ 看看,就會分別得到 $10^6$ 和 $10^{10}$,而使用電腦一秒可以執行 $10^9$ 次基礎運算的基準去衡量的話,就會很明顯的看出 $n=10^5$ 肯定跑不進一秒了!
認識完時間複雜度後,我們就可以來學習如何計算時間複雜度了。想像我們打算寫出上面那段程式,我們在腦袋中想的會是什麼呢?
我要跑一個迴圈,
i從0到n-2
每次我會依序檢查前n-i-1個位置
如果前一項大於後一項,就交換這兩個位置上的數字
有上述思路後,複雜度的計算就呼之欲出了:迴圈要跑 $n$ 次、每次檢查至多 $n$ 次、交換是瞬間的,所以就大約是 $n\times n$,時間複雜度為 $O(n^2)$!
讀者可以注意到,上述的計算我們也不在乎什麼 n-i-1 這種詳細的次數,反正他也只會造成係數上的差距而已,不如就直接當成 n 就行了。
是不是單純多了呢?
總不可能每次寫程式都只有簡單的幾層迴圈吧?就好比在執行完上面的程式後,如果還要輸出整個陣列的樣子的話,就要多花 $O(n)$ 的時間將其輸出出來,那這樣的時間複雜度是多少呢?
讀者可以當成我們是直接在進行「相加」的運算,也就是試著直接求 $O(n^2) + O(n)$ 是多少!這時,比較弱的項可以被丟棄,因此就會直接得到 $O(n^2)$ 這個答案。
「相乘」在複雜度上也是沒問題的,而其實我們早就偷偷用過相關的概念了。前述的例子其實就是一個典型的「$O(n)$ 次窮舉,每次執行 $O(n)$ 次的檢查」,所以直接透過 $O(n) \times O(n)$,就能得出 $O(n^2)$ 了。
因此,在分析時間複雜度時,我們可以放心的直接對這些複雜度進行加法跟乘法。
除了程式的執行時間,我們也很在乎這個程式用了多少記憶體,過大的記憶體使用量會導致電腦無法執行。記憶體使用量就是這個程式的空間複雜度,而這會與變數型態、變數數量以及陣列大小有關。
計算空間複雜度的方法與時間複雜度類似,甚至更為單純,我們只需要去估計程式會宣告出來的記憶體量即可,就好比宣告一個長度為 $n$ 的陣列,使用的空間複雜度就至少是 $O(n)$。
由於空間複雜度還不會是初學競賽程式時的重點,這裡就不再多描述,相信讀者在未來的篇章慢慢熟悉後,真的遇到了需要認真分析空間複雜度的狀況也不會太過陌生。
以下透過幾份程式碼,來幫助大家學會分析複雜度。當然,前面也說過實際在比賽時,我們是不會等到寫完程式碼才去分析複雜度的。不過畢竟我們也還沒教過什麼演算法嘛!就讓我們先試著用程式碼來練習分析,等到未來的章節就能看到各式不同演算法是如何被分析的,就能漸漸熟悉了。
為了方便起見,我們會用 $T(n)$ 來表示每一份程式的時間複雜度。
bool is_prime(int n) { // 判斷 n 是否是質數
if (n == 1) return false;
for (int i = 2; i * i <= n; ++i)
if (n % i == 0) return false;
// 若 n 不是質數,假設 n = a * b (a, b > 1),則 min(a, b) * min(a, b) <= a * b = n
// 也就是 n 不是質數若且唯若 n 的其中一個因數會介於 2 到 sqrt(n) 之間或 n = 1
return true;
// 若找不到介於 2 到 sqrt(n) 的因數,則 n 為質數
}
其中特判 n == 1 的部分是 $O(1)$, for 迴圈總共會跑至多 $\sqrt{n}$ 次,而迴圈內的運算每次執行都是 $O(1)$ 時間,因此總時間複雜度為 $T(n) = O(1) + O(\sqrt{n}) \cdot O(1) = O(1) + O(\sqrt{n}) = O(\sqrt{n})$。
空間複雜度的部分,除了 $n$ 以外只多用了一個變數 $i$ ,因此空間複雜度為 $O(1)$。
int solve(int n) {
if (n == 0) return 0;
return solve(n - 1) + 1;
}
在 return 之前的部分時間複雜度為 $O(1)$,因此將可以列出複雜度的遞迴關係為 $T(n) = T(n - 1) + O(1)$,然後繼續往下遞迴可以得知時間複雜度為
\[
\begin{align*}
T(n) &= T(n - 1) + O(1) \\
&= T(n - 2) + 2 \cdot O(1) \\
&= T(n - 3) + 3 \cdot O(1) \\
&= \cdots \\
&= T(0) + n \cdot O(1) \\
&= O(1) + n \cdot O(1) \\
&= O(n)
\end{align*}\]
空間複雜度的部分,雖然看起來沒有用到新的變數,但實際上每次函數中的參數 $n$ 會占用 $O(1)$ 的空間,因此 $n$ 次遞迴加總起來的結果會占用 $O(n)$ 的空間。
再來看一個比較難的例子:
int monotonic_stack(int arr[], int stk[], int n) { // n: arr 陣列的大小
int stk_size = 0;
for (int i = 0; i < n; ++i) {
while (stk_size > 0 && stk[stk_size - 1] <= arr[i]) {
--stk_size;
}
stk[stk_size++] = arr[i];
}
return stk_size;
}
在第四行的 for 迴圈會跑 $n$ 次,由於 stk_size 可能會到 $n$,因此第五行的 while 迴圈可能會被跑 $n$ 次,此時可能會想說時間複雜度就是 $O(n) \times O(n) = O(n^2)$。但實際上不是這樣的,如果我們不是關注每次 for 迴圈時 while 迴圈會被跑幾次,而是關注 while 迴圈總共會被跑幾次呢?
由於每次跑 while 迴圈會讓 stk_size 減去一、卻不會使其 $<0$,又因為 stk_size 頂多只會增加 $n$ 次(因為第七行只會跑 $n$ 次),所以這個 while 迴圈只會被跑過 $n$ 次,因此總時間複雜度 $=$ stk_size 增加次數 $+$ while 迴圈執行次數 $= O(n)$。
空間複雜度的部分,包含了 arr 陣列(大小為 $n$)、變數 n、i 和 stk_size(大小為 $O(1)$)、stk 需要使用到的空間(stk_size 最大只到 $n$),因此加總起來空間複雜度為 $O(n)$。
不過這份程式碼在做什麼呢?相信不久遠的未來就會再看見他了……
也許讀者對於我們省略了這麼多係數和項數還保留著一些存疑,但就好比我們最一開始舉的例子,我們關注的總是「當資料量越來越大時,你的演算法究竟能多快?」,也因此「成長趨勢最快」的那項理當才會變成我們最在乎的。就讓我們用以下圖片來再解釋一下:
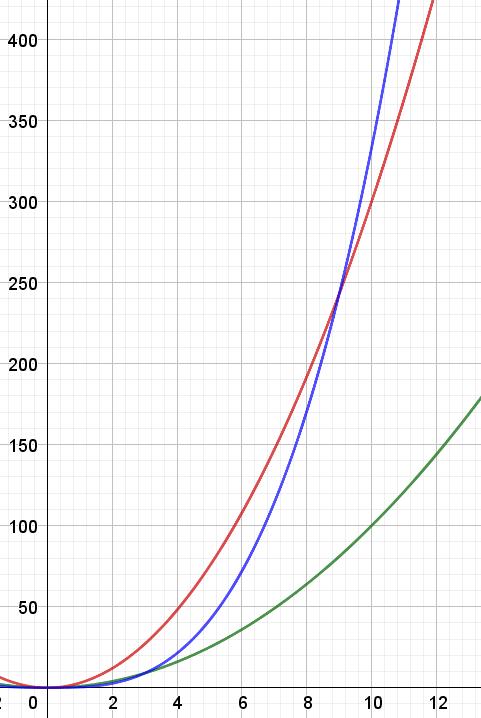
上圖中,綠色曲線符號是 $f(n) = n^2$,紅色曲線是 $g(n) = 3n^2$,藍色曲線是 $h(n) = \frac{1}{3} n^3$,儘管 $h$ 的係數很小,$f, g$ 的係數很大,但由於 $n^3$ 的成長趨勢比 $n^2$ 快,所以當 $n$ 足夠大時 $h(n)$ 還是會比 $f(n)$ 跟 $g(n)$ 大。所以這就是為什麼我們計算時間複雜度時只看成長趨勢最快的那項,並且不過度在意係數的原因。
通常我們在做題目的時候,只會考慮這個做法的複雜度的上限,儘管他在大部分的情況不會達到這個複雜度,我們還是必須考慮最糟的情況,確保每個情況都能在這個複雜度的時間內跑完。就好比以下這份程式碼:
long long solve(int n) {
if (n % 100000 == 0) {
long long sum = 0;
for (int i = 1; i <= n; ++i)
sum += i;
return sum;
}
return 0;
}
他的時間複雜度是多少呢?答案是 $O(n)$ 的!就算 $n$ 不是 $10^5$ 的倍數他會立即結束,只要出題者在題目裡面放上一個 $10^5$ 的倍數當做測試資料,這份程式碼就會因此花費 $n$ 的時間。這也是為什麼我們只在意、也必須在意上限了。
前面我們已經宣導了省略係數的好處,但我們再次把前面分析成 $O(n^2)$ 的程式碼拿回來講:如果我執行這段程式碼 $1000$ 次,那他還能跑進一秒嗎?
假設我們直接用一般的時間複雜度去分析,$1000n^2$,可以省略係數,所以也是 $O(n^2)$ 吧?但如果實際用前面分析出來的 $0.003$ 秒下去算的話,$1000$ 倍的時間就是 $3$ 秒,差距非常慘烈。
這種隱藏在複雜度包裝下、看不見的係數我們又稱為「常數」。實際上,即使是 C++ 的基本運算,還是有一些比較慢的操作。就好比除法跟 % 運算,這兩者的運算速度其實幾乎是加減法的 $5$ 倍以上!而我們最常使用的輸入、輸出其實也非常非常的慢,常常在輸入有 $10^7$ 個數字時,程式就得花費個好幾秒才能輸入完畢。
因此,就算有時候演算法的時間複雜度很好,也還是要稍微考慮一下有沒有可能因為執行了過多倍的運算,導致速度比想像中還要慢一些。就好像如果執行了 $10^5$ 次 $O(n)$ 的演算法,在 $n=10^5$ 的情況下,不就跟 $O(n^2)$ 一樣慢了嗎?
不過其實在初學程式競賽時還不用太過擔心這個問題,還是先分析出單純的時間複雜度才比較要緊。
假設時間限制是 $t$ 秒,而某個做法複雜度是 $O(f(n))$,只要常數不要太大的話,通常我們可以當成只要 $f(n) \leq 10^8\times t$ 就可以通過,有時候順利的話 $10^9\times t$ 也可以通過。
但是還請別忘記,複雜度並不能計算絕對時間,只能計算 $n$ 大小變化時的成長趨勢,常在 $n$ 很小、或是某些特殊情況下時,複雜度大但常數小的演算法反而會跑的比複雜度小但常數大的演算法快,這就是未來各位讀者可能會逐漸體會到的課題了。
由於分析複雜度實在是太過重要,因此競賽選手們時常會直接以輸入的範圍限制,例如 $n$ 的大小上限,並搭配可能的常數大小來判斷自己設計出來的演算法時間複雜度是否吻合於範圍限制,就不用再浪費時間慢慢代入 $n$ 的值來估計執行速度了。
以下皆假設題目的時間限制為 $1$ 秒,用來估算的數字為 $n$:
| 時間複雜度 | 常數大小 | 常見 $n$ 的上限 |
|---|---|---|
| $O(n)$ | 夠小 | $10^7$ |
| $O(n)$ | 略大 | $10^6$ |
| $O(n\log n)$ | 夠小 | $10^6$ |
| $O(n\log n)$ | 一般 | $5\times 10^5$ |
| $O(n\log n)$ | 過大 | $2\times 10^5$ |
| $O(n\log^2 n)$ | 夠小 | $10^5$ |
| $O(n\log^2 n)$ | 一般 | $5\times 10^4$ |
| $O(n^2)$ | 夠小 | $10000$ |
| $O(n^2)$ | 一般 | $5000$ |
| $O(n^2)$ | 略大 | $3000$ |
| $O(n^2\log n)$ | 夠小 | $3000$ |
| $O(n^2\log n)$ | 一般 | $1000$ |
| $O(n^3)$ | 極小 | $1000$ |
| $O(n^3)$ | 一般 | $500$ |
| $O(2^n)$ | 需要仔細評估 | $20\sim 25$ |
當然,上表只不過是一種估計而已,實際狀況還是有不少變化,這裡僅供初學者參考。至於上述「判斷常數大不大」的欄位,常數到底怎樣算大呢?這可能就要各位讀者自行多體會幾次了──總是得在試錯中成長!
另外就是上表提供的參考基準是 $1$ 秒,所以也常可以看到解答是 $O(n\log^2n)$ 的題目將範圍出到 $2\times 10^5$,並直接將時限開到 $5$ 秒等狀況。而根據 Online Judge 的不同,程式碼的執行速度也會有差距,甚至在一些古老的 Judge 上,會出現 $10^6$ 幾乎無法讓 $O(n\log n)$ 通過的現象,所以實際上還是要多遇過幾次狀況才會比較有經驗。
希望大家在想到一個題目的做法時,可以先想想看這個演算法的複雜度是多少,來判斷這個做法寫出的程式大約要執行多久。如果真的很難分析的話,約略估計也可以得到不錯的效果。
順帶一提,我們在複雜度使用的 big-O 符號其實在數學上是真的存在應用的符號,只不過擔心太過複雜,我們省略了較為嚴謹的數學定義和敘述。等到未來的篇章,我們會再次提起他們並詳細解釋一遍。