遞迴從程式的角度來解釋，指的是一個函式在執行過程中會呼叫自己，使得函式中的程式碼會被反覆執行。直到達成某個條件後，這個函式才會停止呼叫自己，並完成執行後回傳，從而結束遞迴的過程。

簡單舉一個例子，想像一下在走迷宮時，我們會不斷遇到路口，如果我們想要用程式來程式來走迷宮，我們便會寫一個函式來處理遇到路口時該做什麼行動。在這個函式中，我們會分別嘗試左轉、直走、或右轉並遇到下一個路口，然後再做一次遇到路口後的行動。這一系列的行為會一直持續下去，直到我們達成了「走到終點」這個條件才會停止。試著將這段口語敘述轉換成程式碼後，看起來會是這樣：

void intersection() {
    if (arrive_exit) {
        win();
        return;
    }
    if (left_enable) {
        turn_left();
        intersection();
    }
    if (right_enable) {
        turn_right();
        intersection();
    }
    if (forward_enable) {
        move_forward();
        intersection();
    }
    return;
}

遞迴函式通常會在我們需要解決具有多個層次的問題時被使用。在迷宮這個例子中，每個十字路口都是一層問題，當我們選擇往一個方向走後，便會遇到下一個十字路口，也就是下一層問題。由於我們一開始不知道走完迷宮總共需要解決幾層十字路口的問題，這時候就會使用遞迴這個技巧。我們可以使用一個遞迴函式來解決一層十字路口的問題，而這個遞迴函式遇到下一個十字路口，也就是下一層問題時，就會再呼叫一次自己這個函式，來解決新的一層問題。

另外，在這個遞迴函式中我們也可以發現，如果到了一個十字路口時，它的左邊、前方、右邊都沒有路，也就是到了一個死路後，函式便會停止前往新的十字路口，並回到上一個十字路口。這就是遞迴中最重要的概念，「遞迴終止條件」。遞迴終止條件往往是我們在寫遞迴時第一件要考慮的事情，一來它能夠避免遞迴函式不知道要停下來而一直遞迴下去，形成無窮遞迴。二來這個條件也能幫助我們思考遞迴函式解決問題的條件，詳細考慮什麼情況才算是完成遞迴，能夠更好理解題目。

在撰寫遞迴函式時，有一個要點是，只需要考慮在解決這一層問題時需要注意的事就好，不要試圖連下一層的情況也考慮進去，否則你會讓你的腦袋跑進一個無窮遞迴。當我們遇到需要進入下一層問題的情況時，直接把自己這個遞迴函式放上去就行。寫遞迴函式時要一邊假裝這個函式已經寫好，一邊完成這個函式的實作。就像在迷宮的例子中，我們假裝 intersection 已經寫好了，這樣左轉、直走、或右轉後遇到新的十字路口，我們就可以直接用已經「寫好」的 intersection 解決了。

既然我們提到了遞迴通常是用來處理有多個層次的問題，那麼具體而言會像是怎麼樣的題目呢，就讓我們來看一些例子吧：

從上述關係式可以知道，要求出費波那契數列的第 $n$ 項 $F(n)$，就必須求出 $F(n-1), F(n-2)$，而要求出 $F(n-1)$，我們就會需要知道 $F(n-2), F(n-3)$，一路求到 $F(0), F(1)$為止。因此，我們可以把費波那契數列的每一項都看成一層問題，再利用遞迴來解決每一層問題。

來考慮一下前面提到的兩個重點：

• 遞迴終止條件：對於 $F(n)$ 的計算，只要計算完 $F(n-1)$，$F(n-2)$ 就可完成遞迴並回傳。除此之外 $n = 0$ 和 $n = 1$ 會有比較特別的終止條件，因為他們的數值是在最初被規定好的，所以直接回傳就好了。
• 撰寫遞迴函式：我們假裝遞迴函式已經寫好，就可以簡單把函式計算 $F(n)$ 的步驟直接寫成 $F(n-1) + F(n-2)$ 了！

int fib(int n) {
    if (n == 0) return 0;
    if (n == 1) return 1;
    return fib(n - 1) + fib(n - 2);
}

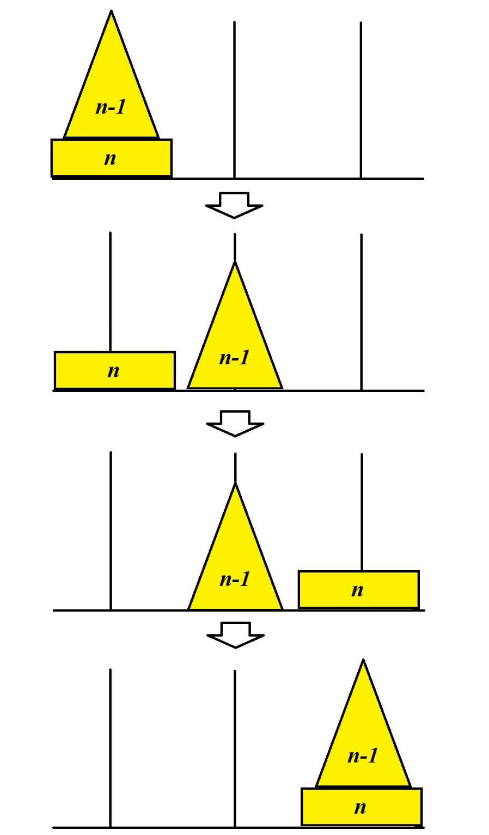
我們先來簡單了解一下河內塔的遊戲策略，首先，遊戲一開始的第一個目標，便是想辦法把最大的盤子從最左邊移動到最右邊。而要能夠完成這個目標，我們必須把最小的盤子到第二大的盤子都搬到中間。同樣的，要達成這個目標，我們要能夠把第二大的盤子放到中間，在那之前，要先把最小的盤子到第三大的盤子移動到右邊。降到這邊，相信大家已經看出來題目所具有的層次性了。我們可以將「把最小的盤子道第 $n$ 個盤子從 $a$ 柱子移動到 $b$ 柱子」看成一層問題，並用遞迴來解決這個問題。在撰寫程式的時候後，我們同樣要注意兩個技巧：

• 遞迴終止條件：為了移動大盤子，我們會需要去遞迴移動小盤子。顯而易見地，我們會在移動最小的盤子時結束遞迴。
• 撰寫遞迴函式：假裝移動「小」河內塔的函式已經寫好，那我們移動「大」河內塔的步驟便是：移動「小」河內塔到空的臨時柱子 $\rightarrow$ 把「大」盤子移動到目標柱子 $\rightarrow$ 移動「小」河內塔到目標柱子、也是「大」盤子上面。

void move(int a, int b) {
    static int steps = 0;
    ++steps;
    cout << "#" << steps << " : move the dish from #" << a << " to #" << b << "\n";
}
void hanoi(int n, int a, int b, int c) { // 將前 n 個盤子從 a 移動到 b，c 是無關的那跟柱子
    if (n == 1) {
        move(a, b);
        return; 
    }
    hanoi(n - 1, a, c, b);
    move(a, b);
    hanoi(n - 1, c, b, a);
}