大家有玩過猜數字遊戲嗎？遊戲的規則是這樣的：主持人會在心中默想一個特定範圍的數字、玩家的任務就是要猜出主持人心中想的那個數字。而每當玩家猜一個數字時，主持人就會告訴玩家他想的數字跟玩家猜的數字之間的大小關係。

你會採用什麼樣的策略來猜呢？換句話說，你會如何「搜尋」出答案呢？接下來我們就要來探討幾種關於搜尋的演算法：線性搜尋法與二分搜尋法。

對於剛剛的猜數字遊戲，我們有一種最粗暴的作法：從第一個數字一路猜到最後一個數字，我們總有一天會猜中！而這樣的作法有一個正式的名稱，叫做線性搜尋法，顯然在目標存在的狀況下都不會出錯，那麼效率如何呢？

對於一個長度為 $N$ 的序列，若是我們想要找到裡面的某個元素，由於我們是一個一個找，因此在最糟的情況下會需要將序列中的 $N$ 個元素都檢查過一次，因此時間複雜度為 $O(N)$。非常直覺的作法，只可惜……效率好像有點差強人意。

寫成程式碼大概像這個樣子：

// arr 是我們要搜尋的序列、len 是序列的長度、tar 是我們要搜尋的目標。
// 回傳值為目標的索引值。
int linear_search (int arr[], int len, int tar) {
    for (int i = 0; i < len; ++i) {  // 暴力檢查每個位置
        if (arr[i] == tar) return i;   // 找到答案後直接回傳
    }
    return len;                       // 沒找到，回傳 len。
}

然而我們會發現剛剛的作法根本就沒有用到主持人提供的資訊。因此我們接下來就來看看猜數字遊戲最廣為人知的一種策略，也就是每次都猜一半，舉例來說，假設這次的數字範圍是 0 到 100，我們就會猜中間的數字，也就是 50、此時如果主持人說要再大一點，我們就會挑選 50 與 100 的中間，也就是 75 作為我們的第二次猜測。以此類推，直到猜出答案為止。這樣的作法就是所謂的二分搜尋法。

為了讓我們等一下把這個過程寫成程式時輕鬆一點，我們先模擬一次整個過程好了，假設真正的答案是 42，我們一開始知道答案是 $0,1,\dots,100$ 之間的某個數，那麼過程是：

• $0,1,\dots,100$ 正中間的數是 $50$，猜 $50$，主持人說要小一點，所以答案在 $0,1,\dots,49$ 裡面。
• $0,1,\dots,49$ 正中間的數是 $24$（我們直接用 $\lfloor \frac{0+49}{2} \rfloor$ 算），猜 $24$，主持人說要大一點，所以答案在 $25,\dots,49$ 裡面。
• $25,\dots,49$ 正中間的數是 $37$，猜 $37$，主持人說要大一點，所以答案在 $38,\dots,49$ 裡面。
• $38,\dots,49$ 正中間的數是 $43$，猜 $43$，主持人說要小一點，所以答案在 $38,\dots,42$ 裡面。
• $38,\dots,42$ 正中間的數是 $40$，猜 $40$，主持人說要大一點，所以答案在 $41,42$ 裡面。
• $41,42$ 正中間的數是 $41$，猜 $41$，主持人說要大一點，所以答案在 $42$ 裡面。
• 候選答案只剩下 $42$ 了，所以答案就是 $42$。

系統化描述一下我們做的事情，在每次要猜的時候，我們都知道答案在一些連續數字 $\ell,\ell + 1, \dots, r$ 之間，要是 $\ell = r$ 也就是「候選答案」裡面只剩一個數字了，那也就只有它可以是答案了，否則我們就猜中間的數字 $m=\lfloor \frac{\ell + r}{2} \rfloor$，然後：

• 如果猜中了，那就猜中了。
• 如果主持人說小一點，那新的候選答案是 $\ell,\ell+1,\dots,m-1$，讓 $r=m-1$。
• 如果主持人說大一點，那新的候選答案是 $m+1,m+2,\dots,r$，讓 $\ell=m+1$。

換一個遊戲，主持人有一個藏起來的非嚴格遞增陣列 $x_1,x_2,\dots,x_n$，它滿足 $x_1 \leq x_2 \leq \dots \leq x_n$，主持人要你猜這裡面第一個 $\geq k$ 的數字是哪一個，一開始你知道的只有陣列的長度 $n$ 和 $k$，然後你每次可以問主持人某一個 $x_i$ 是多少。這個遊戲其實跟猜數字遊戲差不多，作為答案的那個 $x_i$ 的 index $i$ 就像是我們在原版猜數字遊戲裡要猜的那個答案，而一開始的候選答案是 $1,2,\dots,n$，我們每次問主持人一個數字 $m$，我們可以從 $x_m$ 的大小來判斷真正的答案是比較後面還是比較前面。假設我們現在的候選答案是 $\ell,\ell+1,\dots,m$，那麼：

• 如果 $x_m < k$，那答案當然是要比 $m$ 還後面了，新的候選答案是 $m+1,m+2,\dots,r$，讓 $\ell=m+1$。
• 如果 $x_m \geq k$，好像跟剛才有點不一樣，其實 $m$ 還是有可能會是答案，我們只知道 $m+1,m+2,\dots,r$ 都不會是答案了，所以新的候選答案是 $\ell,\ell+1,\dots,m$，讓 $r=m$。

唯一跟原版猜數字遊戲不一樣的點，就是在原版的遊戲裡面，猜中答案時主持人會告訴我們猜中了，但是在這裡不會，就算是看到一個 $x_m=k$ 的數字，我們也不能直接說 $m$ 就是答案，因為有可能 $x_{m-1}=x_m$。當然也有一種方法是如果 $x_m \geq k$ 的話就也問一下 $x_{m-1}$，如果 $x_{m-1} < k$ 我們就知道答案是 $x_m$ 了，反之 $x_m$ 絕不是答案，可以就像原版遊戲那樣把 $r$ 改成 $m-1$，缺點是問問題的次數會變成本來的兩倍，太虧了。不過答案總是存在的，照上述的作法，總有一天候選答案會只剩一個，也就是當 $\ell=r$ 時，這個數字就是答案了。

// 在 arr[1] <= arr[2] <= ... <= arr[len] 中找第一個 >= k 的數字
int binary_search_1(int arr[], int len, int k) {
    int l = 1, r = len;
    while (l < r) {
        int m = (l + r) / 2;
        if (arr[m] < k) l = m + 1;
        else r = m;
    }
    return l;
}

總之，核心概念就是在詢問 $m$ 之後決定一下候選答案的區間會怎麼改變，每次都有其中一半會被砍掉，至於中間我們的詢問點 $m$，要多想一下它還可不可以是答案，這會根據題目而有點不同，像是我們把目標改成找「最後一個 $< k$ 的 $x_i$」，就會變成

• 如果 $x_m < k$，那新的候選答案變成 $m,m+1,\dots,r$。
• 如果 $x_m \geq k$，那新的候選答案變成 $\ell,\ell+1,\dots,m-1$。

有一個要注意的點是如果 $m$ 取 $\lfloor \frac{\ell + r}{2} \rfloor$，那 $r=\ell+1$ 時，$m$ 會是 $\ell$，這個時候要是 $x_m < k$，我們就會把 $\ell$ 改成 $m$……從此陷入無窮迴圈，所以要取 $m=\lceil \frac{\ell + r}{2} \rceil$ 才不會壞掉。還有一件更可怕的事情是，要是哪天候選答案有負數，然後寫成 m = (l + r) / 2，因為除法是向零取整，這在 l + r >= 0 時是下高斯，反之是上高斯，太可怕了！

想那麼多不覺得很麻煩嗎？我們接下來介紹一個更通用也比較不容易出事的寫法。

原版的猜數字問題中，數字有三類：比答案小、答案、比答案大，而找到第一個 $x_i \geq k$ 的版本中，數字只有兩類：$< k$、$\geq k$，答案是第一個 $\geq k$ 的。其實原版猜數字問題中，我們也可以只分兩類：$< $ 答案 和 $\geq$ 答案，而答案就是 $\geq$ 答案之中的第一個（當然也可以把答案分到左邊那一類，變成找左邊的最後一個）。這樣一說，我們做的事情一直都是「把所有候選答案分成兩類，一類都在左邊、另一類都在右邊，目標是找到左邊的最後一個或右邊的第一個」。

剛剛會造成到底是把 $\ell$ 改成 $m$ 還是 $m+1$、$r$ 改成 $m-1$ 還是 $m$、要取上高斯還是下高斯這些問題的最大禍源，就是答案是左邊最後一個還是右邊第一個的差別，所以不如我們就先不要想答案要找哪一個，我們就專注於在找「左邊那類最後一個」和「右邊那類第一個」，稍微修改一下 $\ell$、$r$ 的意思，$\ell$ 是「我們已知的屬於左邊那類的最後一個數字」、$r$ 是「我們已知的屬於右邊那類的第一個數字」，$\leq \ell$ 的我們知道都是左邊那類、$\geq r$ 的都是右邊那類，而中間的都不知道，所以我們就在中間問一個數字 $m$，根據它在哪一類，決定要改 $\ell$ 還是 $r$，$m$ 該是左邊就把 $\ell$ 改成 $m$、該在右邊就把 $r$ 改成 $m$。

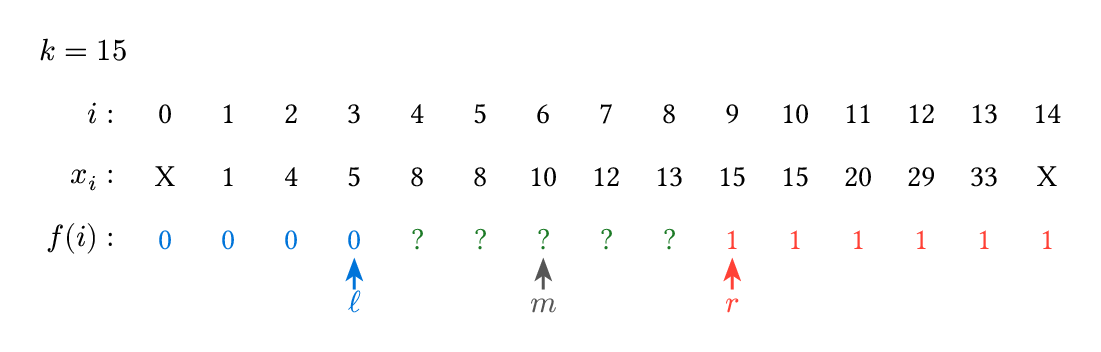
$f(i)$ 的意思是 $x_i$ 這個數字應該屬於左邊那一類還是右邊那一類，$0$ 代表左邊、$1$ 代表右邊，問號代表還不知道。（示意圖，非當事二分搜，這張圖裡的狀態實際上不會在過程中出現，真正的二分搜過程可以看下面的動圖。）

直到 $\ell+1=m$ 時，我們就知道全部的數字在哪一類，左邊的最後一個是 $\ell$、右邊的第一個是 $r$，這時再去想我們要哪一個：第一個 $\geq k$ 的數字就是右邊那類的第一個，也就是 $r$。

// 在 arr[1] <= arr[2] <= ... <= arr[len] 中找第一個 >= k 的數字
int binary_search_2(int arr[], int len, int k) {
    int l = 0, r = len + 1;
    while (l + 1 < r) {
        int m = (l + r) / 2;
        if (arr[m] < k) l = m; // m 在左邊
        else r = m; // m 在右邊
    }
    return r; // 我們要的是右邊那類的第一個
}

注意到我們要搜尋的範圍只有 $x_1,x_2,\dots,x_n$，在這個程式碼裡我們卻讓一開始 $\ell=0$、$r=n+1$，這麼做是因為一開始的 $\ell$ 一定要是在左邊那類、$r$ 一定要是在右邊那類，但其實我們在問問題之前，是不能確定 $x_1$ 或 $x_n$ 在哪一類的，這非常好解決，只要假裝 $0$ 一定是左邊那類、$n+1$ 一定是右邊那類就沒有問題了（同理，在 index 是 $0,1,\dots,n-1$ 時，也可以讓 $\ell=-1,r=n$）。讀者可以自己驗證看看，$m$ 無論是取 $\lfloor\frac{\ell+r}{2}\rfloor$ 還是 $\lceil\frac{\ell+r}{2}\rceil$，都會滿足 $\ell < m < r$，所以往外多開一格並不會造成戳到陣列外面之類的問題，甚至要向哪邊取整都隨便，非常安全，不容易寫錯。

以下這張圖是一個 $n=14$、$k=15$、$x_i$ 如圖所示的範例過程。

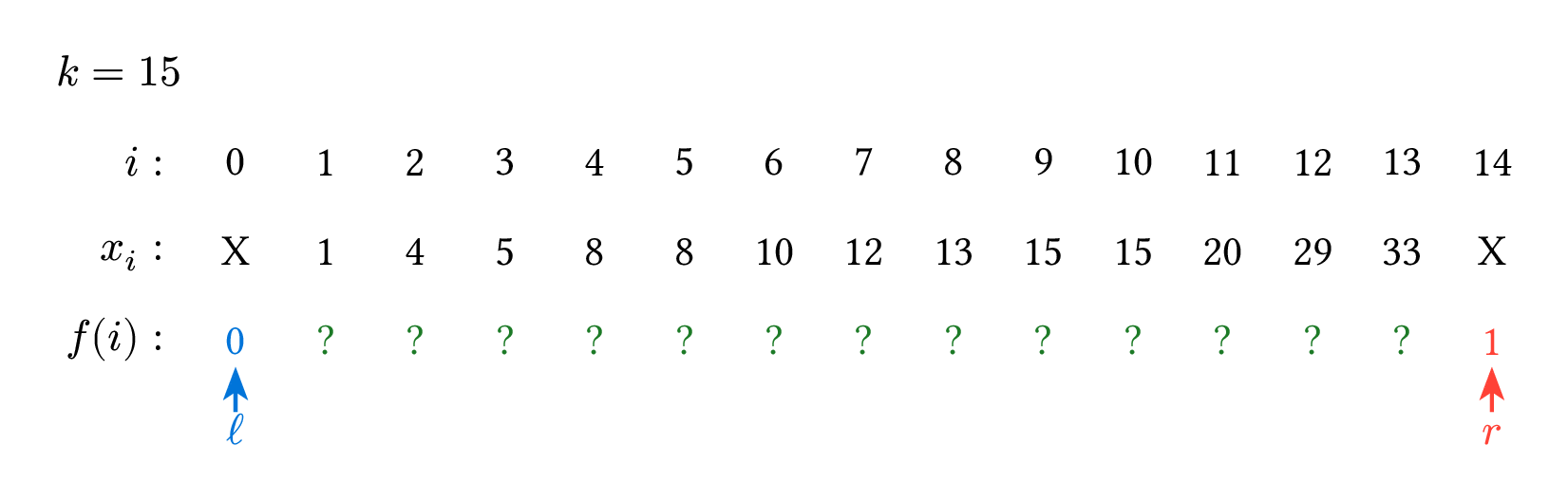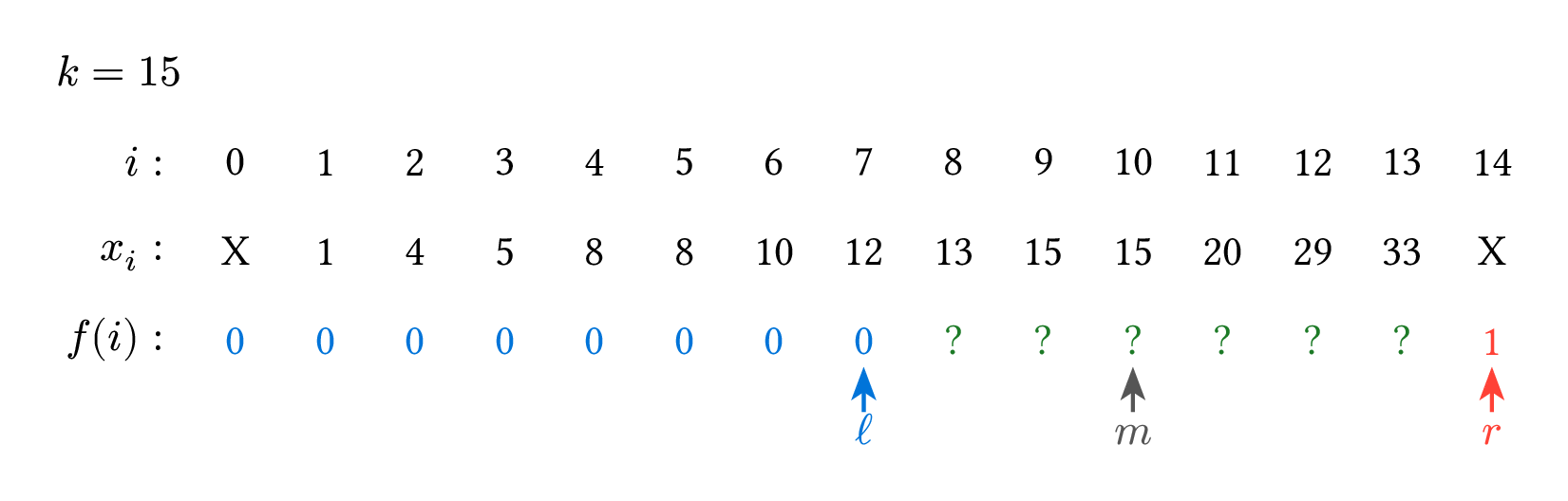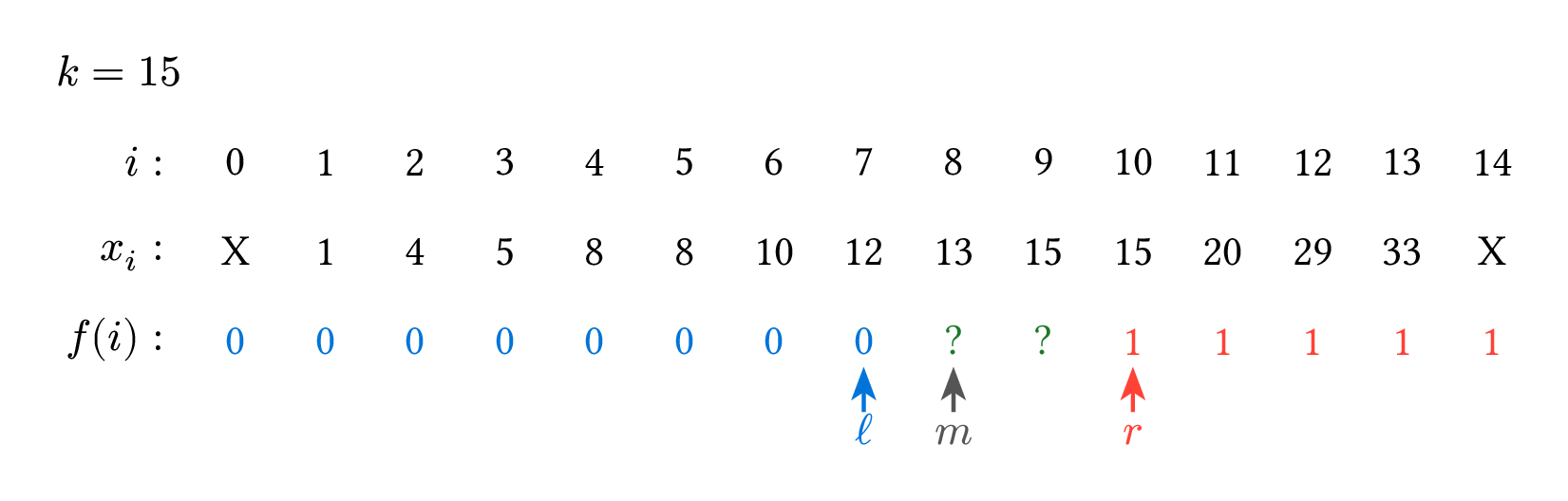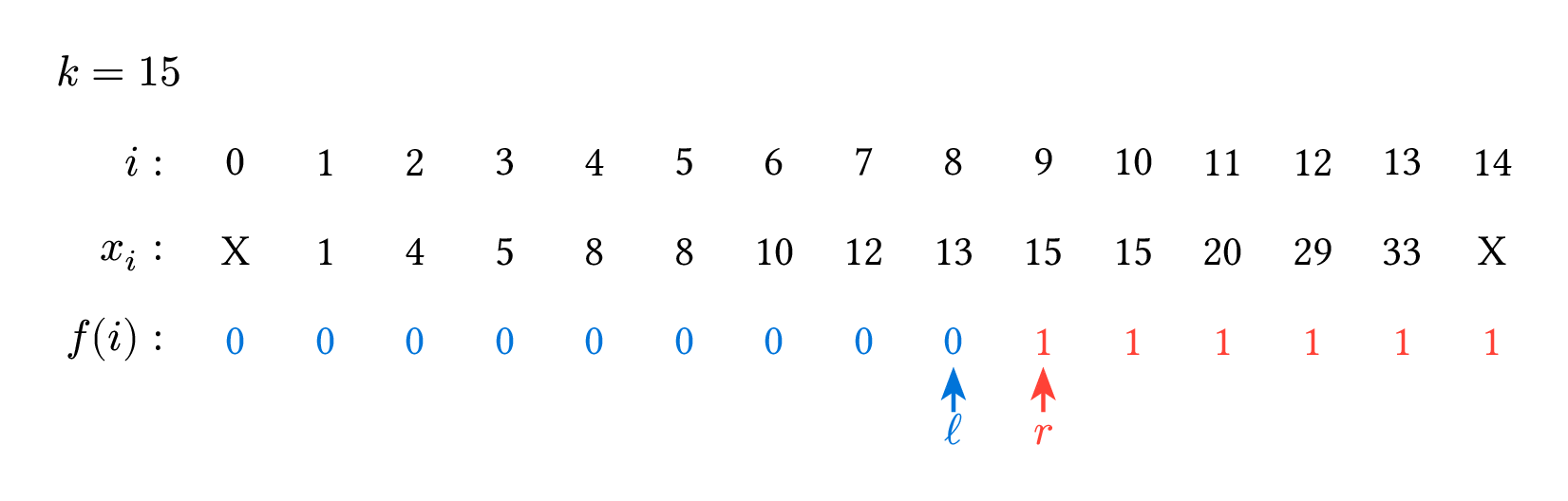
二分搜的本質其實就只有這樣：把數字分成左邊和右邊兩類，然後試圖找出左右兩類的交界點，要寫二分搜時，先好好指出左右兩類的分類依據是什麼，就可以輕鬆寫出程式碼了。剛才說的 $f(i)$ 就是程式碼裡的 arr[m] < k 為 true 時是 $0$，反之是 $1$。當判斷條件比較複雜時，也可以把 $f(i)$ 單獨寫成一個函數。

我們很直覺的會覺得這樣做會比線性搜尋法更好，但究竟好了多少呢？

每次問問題之後，「不知道」的數量就少了一半，舉例來說，本來 $\ell=0$、$r=100$ 的話，中間本來有 99 個不知道在左邊還是右邊的東西，只要問 $m=50$，我們馬上就會知道 $1 \sim 50$ 都是屬於左邊，或者 $50 \sim 99$ 都屬於右邊，馬上就多知道了 50 個！當一開始的搜尋範圍是 $N$（有 $N$ 個未知的東西），那最慘只要用 $\lceil \log_2 N \rceil = O(\log N)$ 次，就可以問清楚每個數字屬於哪一側了。

因此我們得到了 $O(\log N)$ 的複雜度，比線性搜尋法快上不少，既然如此，那為什麼會需要線性搜尋法呢？原因是二分搜的目標序列，必須能好好地被分成左右兩半，舉例來說，如果今天是在一個雜亂無章、沒有排序的序列上，想要找到第一個 $\geq k$ 的數字，因為 $< k$ 和 $\geq k$ 的數字交錯穿插在序列之中，我們就不能用像剛才的方式只問一次問題，就得知某一半的數字都是屬於同一邊了。

其實，在一個有排序的序列上，找到第一個 $\geq k$ 的數這類的需求很常見，難道每次都要寫自己一次二分搜嗎？別擔心，STL 已經幫我們寫好了好用的二分搜函式囉！

• lower_bound(first, last, val, cmp)：從 [first, last) 中找到第一個元素 element 使得 cmp(element, val) 為 false 的位置。
• upper_bound(first, last, val, cmp)：從 [first, last) 中找到第一個元素 element 使得 cmp(val, element) 為 true 的位置。

關於 first 與 last，我們可以傳入一個陣列的兩個位置，也可以利用 STL 容器的 begin() 與 end() 來代表，另外，cmp 的意義與 std::sort() 的 cmp 相同，而傳入的序列必須要以這個 cmp 的規則排序，至於 cmp 的寫法這裡就不再贅述，以下提供一組範例：

#include <algorithm>
#include <vector>
#include <iostream>

using namespace std;

bool cmp (int a, int b) {
    return a > b;
}

int main () {
    int arr[5] = {1, 3, 3, 5, 8};
    int *lower_pos = lower_bound(arr, arr + 5, 3);
    int *upper_pos = upper_bound(arr, arr + 5, 3);
    cout << "lower_bound of ascending: " << lower_pos - arr << '\n';
    cout << "upper_bound of ascending: " << upper_pos - arr << '\n';

    vector<int> vec = {8, 5, 3, 3, 1};
    auto lo_vec_pos = lower_bound(vec.begin(), vec.end(), 3, cmp);
    auto up_vec_pos = upper_bound(vec.begin(), vec.end(), 3, cmp);
    cout << "lower_bound of descending: " << lo_vec_pos - vec.begin() << '\n';
    cout << "upper_bound of descending: " << up_vec_pos - vec.begin() << '\n';
}

看完了二分搜的寫法，緊接著讓我們來看一下二分搜會如何出現在題目裡吧！

先從我們熟悉的開始看起，也就是在一個序列中進行二分搜：

一開始還看不出這道題目與二分搜有什麼關係，雖然我們可以立刻想到一個 $O(N^3)$ 的暴力作法，但想當然爾會超時，仔細觀察一下，我們會發現當我們在枚舉其中兩個數字時，第三個數字其實也就已經被定下來了，也就是說，我們只要暴力的窮舉其中兩個數字，然後確認我們需要的第三個數字有幾個就可以了！

那麼，我們要如何計算第三個數字的數量呢？這時候就輪到二分搜上場了！我們只要把所有的數字由小到大排好，然後利用 lower_bound() 就可以找到我們的目標了。然而，單用 lower_bound() 我們只能確認我們的目標是否存在、以及在序列中的哪裡而已，萬一我們的目標數字有好幾個該怎麼辦呢？

這個時候我們就可以利用 upper_bound() 了，lower_bound() 會告訴我們第一個大於等於目標的位置、upper_bound() 則會告訴我們第一個大於目標的位置，將兩者相減，我們就可以得到等於目標的長度、也就是目標數字的個數了！

最後只要注意一些使用到重複數字的細節並加以處理就可以通過這一題囉！

搜尋是個大家常常都會需要的功能，不同的搜尋方法有不同的特色，像是線性搜簡單無腦但慢、二分搜有效率但也有所限制。

其中二分搜雖然是個基礎的演算法，但他非常好用，而「把東西切一半」這樣的想法還會在未來的許多資料結構與演算法之中一而再、再而三的出現，所以希望各位讀者看文本文後可以對二分搜有基本的認識，並準備好面對接下來的挑戰！