在看到一個序列的時候，「從左到右枚舉」是一個非常常見的枚舉策略，不只是因為迴圈很好寫，更重要的原因是「某一格的答案」經常對求出它右邊那一格的答案很有幫助，像是我們在前綴和與差分提過的經典問題：

用差分的作法是，令 $d_i=a_i-a_{i-1}$，把 $a_l,\dots,a_r$ 都加上 $x$，就是把 $d_l$ 加去 $x$、$d_{r+1}$ 減去 $x$，最後再還原出 $a_i=d_1+d_2+\dots+d_i$。這個作法其實有一個很直觀的解釋方式，先想像一條有 $n$ 個格子的紙帶，題目給了我們 $q$ 個區間，每個區間都帶有一個權重（就是 $x$），並且是一段連續格子，我們要求的就是「對於紙帶上的每個格子，包含這個格子的區間總和有多大」，然後再想像我們從紙帶上由左往右走，並且記錄包含我們現在所在位置的區間權重總和 $s$。

一開始我們站在格子 $1$ 的左邊（可以想像有多一個格子 $0$，就和做前綴和時我們會多一個 $s_0=0$ 一樣），所以我們現在記錄的數字 $s$ 是 $0$。接下來每當遇到一個區間的左界，就要把 $s$ 加上這個區間的權重，而離開一個區間的右界時，就要把 $s$ 減去這個區間的權重，所以 $l,r,x$ 這個操作的區間帶來的結果就是：我們走到格子 $l$ 的時候 $s$ 被加上 $x$、走到格子 $r+1$ 的時候 $s$ 被減去 $x$，也就是說前面算的 $d_i$，就是走到格子 $i$ 的時候 $s$ 會被改變多少。在計算完這個改變量之後，$s$ 就是答案的 $a_i$。

只要開一個長度為 $n$ 的陣列，來存下走到格子 $1$ 到 $n$ 時，當下所在地的總和改變量，做前綴和就等於我們前面敘述的過程，寫出來就和差分一模一樣，時間複雜度是 $O(n)$。

我們把「從左到右枚舉」這個行為解釋成了「從左邊走到右邊」，在遇到這一類很多區間的問題時，想像我們從左邊走到右邊、維護當下所在地的狀態，是一個很常見的作法。除了在紙帶上面走，也可以在數線上面走。（其實都是差不多的事情！）

如法炮製，想像我們從數線的左邊開始走，因為我們想知道的是「數線上有多長的部分被至少一個線段覆蓋」，所以可能會想要維護我們當下所在的地方，有沒有在至少一條線段裡面。不過這樣會有一個問題，就是要是我們單純只有記錄「有沒有覆蓋」，在遇到一條線段的左端點時，我們當然知道接下來的狀態是「有覆蓋」，但如果是遇到右端點，接下來的狀態不見得會變成「沒有覆蓋」，因為我們可能本來在很多條線段裡，現在只是少了一條而已。因此，我們要維護的應該是「我們現在在幾條線段裡面」。

我們的目標是要知道，當我們記錄的狀態，也就是包含我們現在位置的線段數量 $cnt \geq 1$ 時，走過的路有多長，就是所有線段覆蓋的總長度。要是座標範圍（我們叫它 $C$）很小，那我們可以在走到每一個整數點時，更新好接下來的狀態是什麼以後，如果 $cnt \geq 1$ 就把答案加上 1，也就是走到下一個整數點之間那段路。這題的 $C$ 只到 $10^7$ 所以其實也還可以，但要是 $C$ 到 $10^9$ 甚至 $10^{18}$ 的話要怎麼辦？

事實上，我們只關心「狀態改變的時機」，也就是所有線段端點而已，兩個端點之間如果沒有任何其他線段端點，那也就不會發生狀態改變，因此我們只要知道這一段究竟有沒有被線段覆蓋，有的話把答案加上一整段的長度就好。換句話說，可以想像整條數線被所有端點分成很多段，每一段一起算就好。在實作上，只要把所有端點左到右排序，就可以摸擬在數線上走的過程了。

#include <bits/stdc++.h>
using namespace std;
using pii = pair<int, int>;
int main () {
    ios_base::sync_with_stdio(false);
    cin.tie(0);

    int n;
    cin >> n;
    vector<pii> events;
    for (int i = 0; i < n; i++) {
        int l, r;
        cin >> l >> r;
        events.emplace_back(pii(l, 1));
        events.emplace_back(pii(r, -1));
        // 1 代表左端點，-1 代表右端點
        // 也就是走到那個點時，包住當前位置線段數的改變量
    }
    sort(events.begin(), events.end());
    int cur = 0; // 包住當前位置的線段數
    int ans = 0;
    int lst = -1; // 上一個碰到的端點
    for (auto [x, diff] : events) {
        // 如果前面那一段的是有被包住的，要加上那一段的長度
        if (cur > 0) ans += x - lst;
        cur += diff;
        lst = x;
    }
    cout << ans << "\n";
}

注意到在這裡，我們的實作方法是「走到一個點時看上一段」，因為要知道下一段的長度比較麻煩一點，所以乾脆看上一段。

這種想像自己在走的方法稱為掃描線，就是想像有一條直線掃過去，你就是那條直線。剛剛我們討論的都是一維版本的掃描線，掃描對象是很單純的一個序列（一些格子）配上一些區間，或者一條數線配上一些線段，然後很單純的左往右掃，這種題目的作法框架基本上都差不多，首先先找出你關心的當下狀態，然後看看狀態什麼時候會發生改變，狀態改變的事情就被稱為事件，把事件按照發生時間點（通常就是座標）排序後，就可以好好摸擬掃描的過程，如果座標範圍不大，也可以直接開一個長度是 $C$ 的陣列來直接儲存每個整數時間點發生的事件，並一一枚舉所有整數時間點。

在用掃描線的時候，我們需要有一個起始狀態，在線段覆蓋長度的程式碼裡，lst 的初始值是 $-1$，可以理解成是我們假設起點是 $-1$，而起始狀態是包住現在位置（也就是起點）的線段數量是 $0$。通常只要挑一個在所有端點左邊的點當起點就好，而在對序列掃描時，可以自己加一個 index 是 0 的位置當起點。

在處理任何區間相關問題的時候，都要特別注意邊界究竟有沒有被包含。舉剛剛的例子：

• 在區間加值問題中，一個區間 $[l,r]$ 的意思是對元素 $a_l,a_{l+1},\dots,a_r$ 加值，區間內的總元素數量是 $r-l+1$，進入區間的時間是走到第 $l$ 個元素的時候，離開區間的時間是走到第 $r+1$ 個元素的時候。
• 在線段覆蓋長度中，一個線段 $[l,r]$ 的意思就是數線上 $[l,r]$ 的範圍，注意到因為這裡關心的是長度，因此在單一一個點上面的狀態並不重要，我們只在乎每個時間點之間的狀態而已，進入區間的時間是走過 $l$ 以後，離開區間的時間是走過 $r$ 以後。

這兩題的差別並不是在區間和線段，而是我們關心的時間到底是每一個點上還是點與點之間，總之就是要仔細想一想，每個事件到底是在什麼時候發生。

剛才的兩個例題中，其實都有同時發生的事件。在區間加值問題中，我們直接用一個陣列來記錄某一刻會發生的所有事件一起造成的效果（所在地的總和會改變多少），所以我們確確實實地讓同時發生的事件一起發生了，不過在線段覆蓋長度中，我們並沒有對位置相同的端點做任何特殊處理，某種程度來說它們就不是同時發生的。舉例來說，我們有四個線段：$(1,3),(2,3),(3,4),(3,5)$，這樣排序過後的 events 就會長成：
\[ (1, 1) \quad (2, 1) \quad \color{red}{(3, -1) \quad (3, -1) \quad (3, 1) \quad (3, 1)} \quad (4, -1) \quad (5, -1) \]
因為 pair 比較時，如果第一項相同，會再比第二項，因此所有同時發生的事件中，右端點（離開事件）會先被處理到，然後才處理左端點（進入事件）。其實這根本就不會怎麼樣，因為我們真正關心的是點與點之間的狀態，而非點上的狀態，因此在時間點 $3$ 上面發生什麼都沒有差，只要走到 $3$ 之前的狀態和走到 $3$ 之後的狀態正確就好了。即便在處理完第二個 $(3,-1)$ 之後 cur 會變成 $0$，走到緊接著的 $(3,1)$ 時就會把答案加上它們兩個之間的長度，但它們之間的長度根本就是 $0$，無論如何都不會對答案有所影響，就算時間一樣的事件亂排，不要照第二項排序都沒有關係。

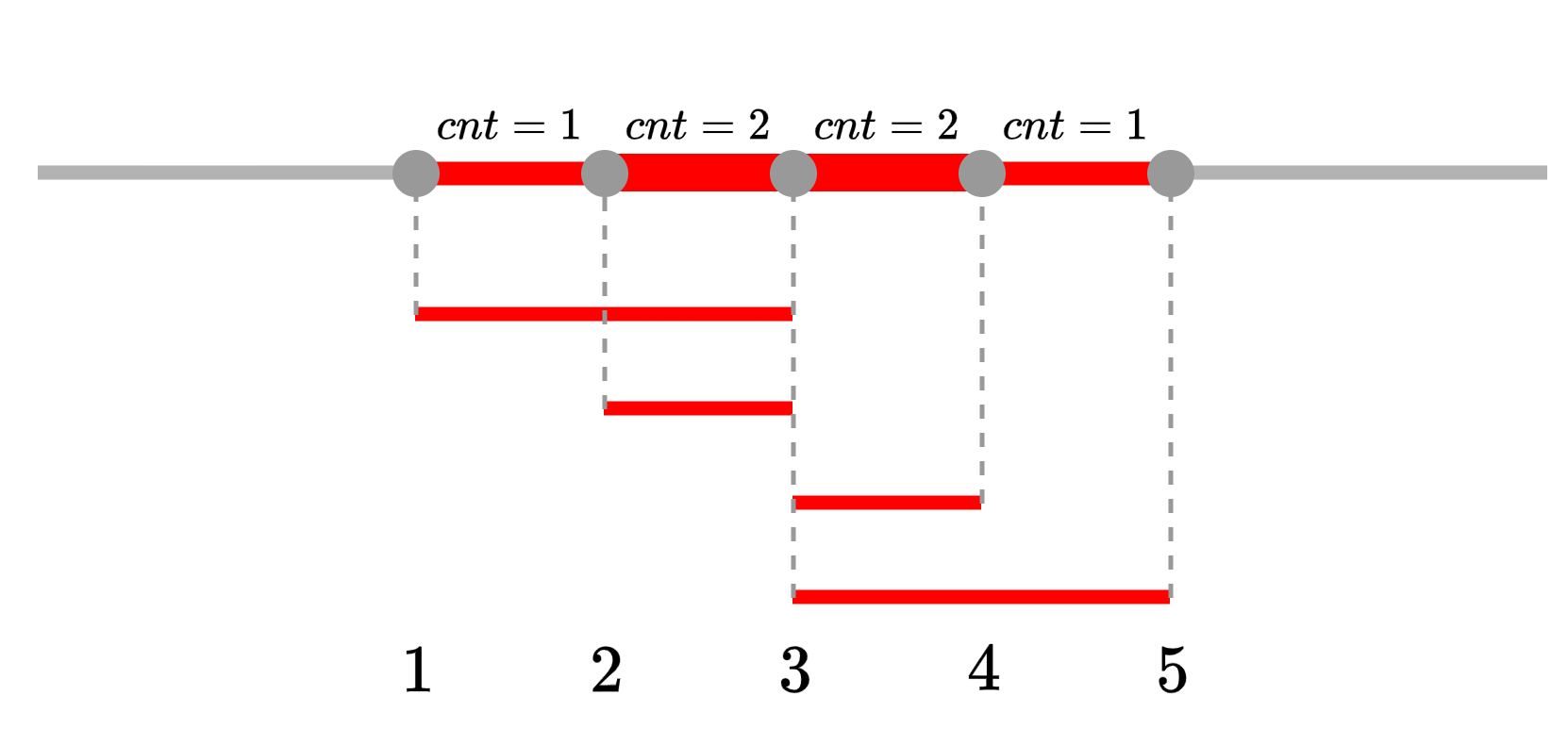
不過，並不是所有題目都能這樣亂排序。舉例來說，我們把題目改成問「給一些左閉右閉區間，是不是所有區間的聯集，是一個連續的區間」，如果是剛剛舉的那四條線段直接當成端點一樣的閉區間，它們的聯集是 $[1,5]$，因此答案是 Yes，但要是我們直接把區間覆蓋問題的作法改成「在碰到第一個事件以後，最後一個事件以前，有任何時候 cur 變成 $0$，答案就是 No，都沒有就是 Yes」，那就會獲得一個 WA，因為處理完第二個 $(3,-1)$ 後 cur 就會短暫地變成 $0$。

一種處理方式是改變排序順序，我們讓同時發生的事件中，進入事件先發生，然後才發生離開事件，就不會遇到這個問題。另一種選擇是真的把同時發生的事件一起處理好，再去算答案，比較直覺的方法是直接用一個 map<int, vector<int>> 存每個時間點發生的每個事件（在這題也可以把 vector<int> 換成只用一個 int 存總和），但是 map 很慢，只用 vector 加上 sort 的方法是：

sort(events.begin(), events.end());
int cur = 0; // 包住當前位置的線段數
bool ans = true;
for (int i = 0; i < (int)events.size(); ) { // 不要有 i++！
    int x = events[i].first; // 目前時間點
    // 所有在時間點 x 發生的事件
    for (; i < (int)events.size() && events[i].first == x; i++)
        cur += events[i].second;
    // 跑完上面這個迴圈以後，i 會是第一個時間 > x 的事件
    // cur 變成 0 了卻還沒走完最後一個事件
    if (cur == 0 && i < (int)events.size()) ans = false;
}

這樣就可以直接抓出所有同時發生的事件一併處理。

剛剛我們會發生的事件只有兩種：走進一條線段和走出一條線段，有時候事件會更複雜，例如：

詢問點也是數線上的一個點，把「遇到詢問點」也當成是一種事件的話，現在我們的事件有三種：在 $l_i$ 進入線段 $i$、在 $r_i$ 離開線段 $i$、在 $q_i$ 記錄現在在的地方被幾條線段包含。當有多種事件的時候，就要特別注意同時發生的事件的處理順序，由於線段是閉區間，正確的處理順序是先處理進入線段事件、處理詢問事件，最後再處理離開線段事件。注意這個順序會跟你設計的邊界有關，如果是想成「因為 $r_i+1$ 是第一個不在線段 $i$ 裡的整數點，所以離開線段 $i$ 的時間是 $r_i+1$」，那正確的順序就是最後再處理詢問事件。

實作的時候，當然可以用前面提到抓出所有同時發生的事件一併處理的方式，好好地把所有在一個時間點的事件都拿出來後，再寫三個迴圈分別處理三種事件，但這樣終究是有點麻煩，因此也可以直接把同時的事件按照類型用正確的順序排序。

#include <bits/stdc++.h>
using namespace std;
struct event {
    // type 0: 進入, 1: 詢問, 2: 離開
    // type 0,2 的 id 其實不會用到
    int time, type, id;
};
bool operator<(event a, event b) {
    if (a.time != b.time) return a.time < b.time;
    return a.type < b.type; // 同時的事件照類型排序
}
int main () {
    ios_base::sync_with_stdio(false);
    cin.tie(0);

    int n;
    cin >> n;
    vector<event> events;
    for (int i = 0; i < n; i++) {
        int l, r;
        cin >> l >> r;
        events.emplace_back(event({l, 0, i}));
        events.emplace_back(event({r, 2, i}));
    }
    int q;
    cin >> q;
    for (int i = 0; i < q; i++) {
        int x;
        cin >> x;
        events.emplace_back(event({x, 1, i}));
    }
    sort(events.begin(), events.end());

    int cur = 0; // 包住當前位置的線段數
    vector<int> ans(q);
    for (auto [time, type, id] : events) {
        if (type == 0) cur++;
        else if(type == 2) cur--;
        else ans[id] = cur;
    }
    for (int i = 0; i < q; i++) cout << ans[i] << "\n";
}

在需要排序帶有有點多資訊的物件的時候，可以善加利用 struct，而不是使用 tuple 或很多層 pair，雖然 pair 或 tuple 自帶比較運算子，但可讀性會很差，也比較容易寫錯。

掃描線是一種把演算法具體化的方式，而不是一種特定的技巧框架，核心精神就只有想像一個移動的過程、嘗試維護當下的狀態，並找出所有會造成狀態改變或者需要記錄狀態的時間點。雖然在上面這些例題中，從左到右掃都是還算顯然的策略，而且也不一定非得要用掃描線去想（像區間加值直接用差分的作法，就不用在腦裡想一個掃描線），不過在更複雜的題目之中，把作法用掃描線這樣的方式具體化往往可以降低思考難度，將來讀者就會慢慢見識到這種方法的厲害之處了。