閱讀本文之前,建議讀者對指標要先有一點基本認識。如果需要學習資源的話,可以看這裡。
二元樹是許多資料結構的基礎,許多複雜和強大的資料結構都是使用了二元樹的概念達到好的時間複雜度。
首先解釋一下什麼是樹。資訊領域中的「樹」是一個由「節點」和「邊」組成的圖。
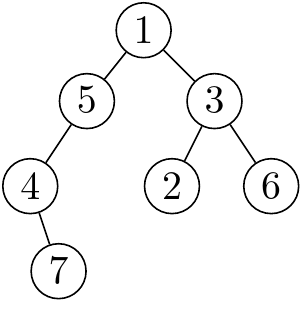
上圖中,每個圓圈是節點(Node/Vertex),上面的數字是節點的編號,每一條線是邊(Edge)。最上面的節點稱作根節點(Root),而對於某一節點 $a$,他往下一條邊連到的點稱為 $a$ 的子節點(Child)。
上面那張圖同時是一個二元樹(Binary Tree),意思就是樹上的每一個點至多有兩個子節點。為什麼我們特別在乎這種樹呢?原因是因為他的架構足夠簡單、方便實作、又有著「樹狀」的性質。
$k$ 元樹的意思就是每個節點至多有 $k$ 個子節點。根據定義,一元樹也是一種樹,但是他其實跟陣列沒兩樣。通常這種樹會被稱作一個鏈(Chain)。
前面提到二元樹的限制就只有是一棵有根的樹、每個節點最多只有兩個子節點,聽起來其實也沒什麼,但要是我們再多加一點限制上去,它就可以成為能夠用來維護一組排序好的數字的厲害資料結構。
樹狀資料結構中,每一個節點通常會維護一筆資料,我們就假設這個資料是一個整數,並且用節點內的數字表示。那麼二元搜尋樹除了得是一個二元樹以外,還要滿足以下條件:
什麼意思?且看圖中分解。以下是對於集合 $\{1, 2, 3, 4, 5, 6, 7\}$ 所建的兩棵二元搜尋樹:
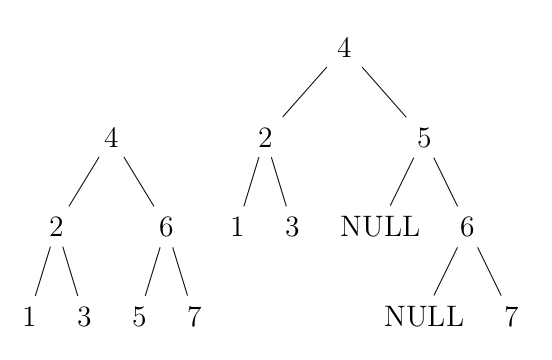
這兩棵樹都是符合以上定義的、裝著我們的集合的二元搜尋樹。在這裡,我們用 NULL 來特別標示那個節點不存在。
這到底可以幹嘛?我們就來看看二元搜尋樹能做些什麼有趣好玩的事。
我們先來想想要怎麼在程式裡存一棵二元搜尋樹。這是一個二元樹的節點,每個節點有三個指標分別指向自己的父節點 parent 以及左右子節點 lson 和 rson。由於我們想要二元搜尋樹上的每個節點維護一個整數,所以我們再多用一個 val 來儲存這個整數。
struct node {
node *parent, *lson, *rson;
int val;
node(const int &data) : parent(NULL), lson(NULL), rson(NULL), val(data) {}
};注意到在二元樹上,你把任何一個節點以下的部分單獨拿出來看,都還會是一個二元樹。所以,每個指向 node 型別的指標都可以視為一棵二元樹的根。當我們要操作一棵二元樹時,其實我們只要有它的根節點,就可以透過根節點存的指標走到整棵樹了,因此我們也直接用代表根節點的 node 來代表整棵二元樹。
一個指標通常需要占 $8$ 個 bytes,所以用指標實作的東西都要花滿多的記憶體,在時間上常數也會比較大。
接下來,我們就來想想要怎麼在維護「二元搜尋樹」性質的同時,操作這個二元樹。
假設已經有一個二元搜尋樹了,那要怎麼插入一個新元素?假設要插入的元素的值為 $x$,且目前走到的節點的值為 $y$(一開始當然是從根節點開始走),那 $x$ 該放在哪裡呢?根據二元搜尋樹的定義,如果 $x < y$,則往左走;反之,則往右走。那如果沒得走了(也就是要走的節點為 NULL),那就在這個位置建立一個新的節點,並且把值設為 $x$。
void Insert(node *&x, int val) {
if (!x) {
x = new node(val);
return x->parent = NULL, void();
}
if (x->val > val) {
if (x->lson) Insert(x->lson, val);
else x->lson = new node(val), x->lson->parent = x;
}
if (x->val < val) {
if (x->rson) Insert(x->rson, val);
else x->rson = new node(val), x->rson->parent = x;
}
}那麼一開始的二元搜尋樹要怎麼建立呢?其實很簡單,如果有 $n$ 個數字 $[a_1, a_2, \cdots ,a_n]$,那就將 $a_1$ 設定為根,再對 $a_2$、$a_3$、……、$a_n$ 等依序插入,插入完了就建立完成!
對於一個陣列,我們可以寫一個 for 迴圈依序看到每一個元素。對於一棵二元搜尋樹,我們則有幾種常見的順序看每一個節點。看每一個節點這件事又稱為遍歷(traversal)。
中序遍歷是二元搜尋樹的遍歷方式之一,他可以將資料結構內部的值按照大小排序輸出。怎麼做到呢?還記得二元搜尋樹的性質嗎?對於任何一個節點,他的左子樹的點一定更小,右子樹的點一定更大。所以對於每一個點,我們都先遍歷他的左子樹,再看他自己,然後遍歷他的右子樹。這樣的順序就會讓數值由小到大輸出。
void travel(node *x) {
if (!x) return;
travel(x->lson);
printf("%d ",x->val);
travel(x->rson);
}另外兩種遍歷方式,下面會再介紹。
在這個二元搜尋樹上,根據值找到節點(或者是查看是否存在,找在樹上最靠近一個值的點之類的),都可以在樹上跑來跑去來搜尋。假設要搜尋的值是 $x$,然後目前所在節點的值是 $y$,那就跟插入一個點的方法一樣:$x < y$ 則往左走,反之則往右走,結束條件就是沒得走或找到了。
node *Find(node *x, int val) {
if (!x) return NULL;
if (x->val == val) return x;
if (x->val > val) return Find(x->lson, val);
return Find(x->rson, val);
}如果想要刪除一個節點,那要分三個情形:依照是不是葉節點(也就是有沒有子節點),可以看出需不需要找替換來遞補原本的節點的位置。如果是葉節點就直接刪掉即可,否則需要找一個替身。作法如下:
bool Delete(node *&root, node *x) {-
如果是葉節點,則直接刪掉。
if (!x) return false; if (!x->lson && !x->rson) { if (x->parent) { if (x->parent->val > x->val) x->parent->lson = NULL: else x->parent->rson = NULL; } delete x; } -
如果其中一個子節點為空,則可以直接拉上來。如下圖:
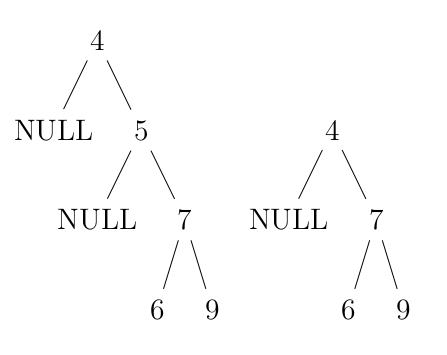
假設要刪除 5,而且他只有一個子樹,那就可以直接把 4 連到 7 就好了(從左圖變成右圖)。
else if (!x->lson) { if (x->parent) { if (x->parent->val > x->val) x->parent->lson = x->rson: else x->parent->rson = x->rson; } else root = x->rson; x->rson->parent = x->parent; delete x; } else if (!x->rson) { if (x->parent) { if (x->parent->val > x->val) x->parent->lson = x->lson: else x->parent->rson = x->lson; } else root = x->lson; x->lson->parent = x->parent; delete x; } -
如果不是,則需要找一個節點當替身。找到的替身要符合:如果將要刪除的節點設為替身的值,並且將替身刪掉之後,還是會符合二分搜尋樹性質。
一種找替身的方法是,看左邊子樹,然後開始往右找到底,直到不能再走了,那就將原本的節點的值換成那個點,然後刪除那個替身。
else { node *exchange = x->lson; while (exchange->rson) exchange = exchange->rson; x->val = exchange->val; // copy the data Delete(root, exchange); }
最後再加上一行就可以了。
return true;當我們要在二元搜尋樹中刪除一個值時,我們可以先找到它,再把節點刪除。
bool Delete_Val(node *&root, int val) {
return Delete(root, Find(root, val));
}整個二元搜尋樹的程式碼在此:
struct node {
node *parent, *lson, *rson;
int val;
node(const int &data) : parent(NULL), lson(NULL), rson(NULL), val(data) {}
};
node *Find(node *x, int val) {
if (!x) return NULL;
if (x->val == val) return x;
if (x->val > val) return Find(x->lson, val);
return Find(x->rson, val);
}
void Insert(node *&x, int val) {
if (!x) {
x = new node(val);
return x->parent = NULL, void();
}
if (x->val > val) {
if (x->lson) Insert(x->lson, val);
else x->lson = new node(val), x->lson->parent = x;
}
if (x->val < val) {
if (x->rson) Insert(x->rson, val);
else x->rson = new node(val), x->rson->parent = x;
}
}
bool Delete(node *&root, node *x) {
if (!x) return false;
if (!x->lson && !x->rson) {
if (x->parent) {
if (x->parent->val > x->val) x->parent->lson = NULL:
else x->parent->rson = NULL;
}
delete x;
}
else if (!x->lson) {
if (x->parent) {
if (x->parent->val > x->val) x->parent->lson = x->rson:
else x->parent->rson = x->rson;
}
else root = x->rson;
x->rson->parent = x->parent;
delete x;
}
else if (!x->rson) {
if (x->parent) {
if (x->parent->val > x->val) x->parent->lson = x->lson:
else x->parent->rson = x->lson;
}
else root = x->lson;
x->lson->parent = x->parent;
delete x;
}
else {
node *exchange = x->lson;
while (exchange->rson) exchange = exchange->rson;
x->val = exchange->val; // copy the data
Delete(root, exchange);
}
return true;
}
bool Delete_Val(node *&root, int val) {
return Delete(root, Find(root, val));
}
void travel(node *x) {
if (!x) return;
travel(x->lson);
printf("%d ",x->val);
travel(x->rson);
}
現在我們要分析一下以上介紹的運算的複雜度:可以知道,如果這棵樹的高度為 $h$(最深的節點深度),則最壞的情況就是在插入或搜尋的時候,每次都遇到最下面的節點,複雜度就是 $O(h)$。那 $h$ 大概會是多少呢?可以觀察:第一層最多可以有 1 個節點,第二層最多可以有 2 個節點,第三層最多可以有 4 個節點……,第 $k$ 層最多可以有 $2^{k-1}$ 個節點,總共可以有 $\sum_{k = 1}^{h} 2^{k - 1} = 2^h - 1$ 個節點,所以
$$n \approx 2^h \implies h \approx \log(n)$$
所以如果是一個夠「平衡」的二元搜尋樹,則搜尋和插入的複雜度都是 $O(\log n)$。
現在我們要對這個序列建立搜尋樹:$[1, 2, 3, 4, \cdots ,n]$,那結果將會是:
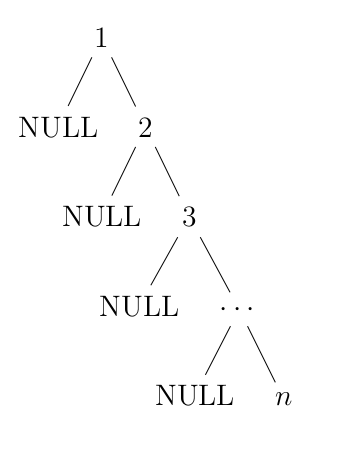
這種情況稱為退化。這樣子的話,$h = n$,而搜尋和插入都變很可悲的 $O(n)$ 了。這樣子的樹就會是「不平衡」的。基於二元搜尋樹的資料結構,通常會有方法避免這種情況。現在就只要祈禱題目是隨機產生不會搞你就好了!
平時要多做好事,才不會比賽的時候被測資雷 (X
測資一定會想辦法卡掉這個,所以才需要平衡二元樹 (O
一個序列依照插入的順序可以排成許多不同的二元搜尋樹,而給你 $N$ 個不同的整數 $a_i$,依序為插入的順序,請問所構成的二元搜尋樹的中序遍歷為何?
條件限制
- $N \leq 10^6$
- $-2^{30} \leq a_i \leq 2^{30}$
有一個一開始是空的集合,接下來有 $N$ 個操作,操作有三種:在集合中加入一個數、刪除一個數,或是詢問離某個數最近的元素是多少,有一樣近的兩個都輸出。
條件限制
- $N \leq 10^5$
- 保證測資是隨機生成的