二元樹可以表示很多種資料的「結構關係」,而我們在處理這種結構的時候,堆疊(Stack)往往會派上用場。
首先,我們先來討論要如何遍歷一個二元樹中的元素。
想要輸出一個二元樹,有三種比較常用的方法:
- 前序 (Preorder):先輸出自己的節點,再照著前序輸出左子樹,再照著前序輸出右子樹
- 中序 (Inorder):先照著中序輸出左子樹,再輸出自己,再照著中序輸出右子樹
- 後序 (Postorder):先照著後序輸出左子樹,再照著後序輸出右子樹,再輸出自己
假設用這個樹來當例子:
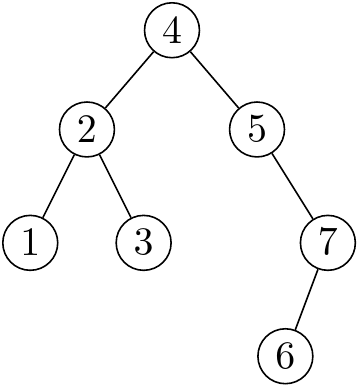
那三種順序分別為:
- 前序:$4, 2, 1, 3, 5, 7, 6$
- 中序:$1, 2, 3, 4, 5, 6, 7$
- 後序:$1, 3, 2, 6, 7, 5, 4$
可以觀察到,中序的數字是從小到大排序的,因此這棵樹是一個二元搜尋樹。
那麼,如果我們只有前序的陣列,而我們已知這棵樹就是二元搜尋樹了,那有沒有辦法還原出這棵樹的長相呢?
讓我們按照前序的方式,一個個把遇到的點畫出來。首先,前序陣列的第一個點一定是根節點。

下一個數字是 $2$,因為他比 $4$ 小,所以他一定是接在 $4$ 的左邊。
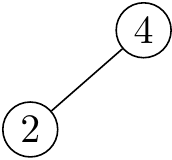
現在我們要考慮 $2$ 底下的點。下一個數字是 $1$,他比 $2$ 小所以在左邊。

現在我們要考慮 $1$ 底下的點。下一個數字是 $3$。我們發現 $3$ 比 $1$ 大,但是他同時也比 $2$ 大,所以他應該要接在 $2$ 的右邊。
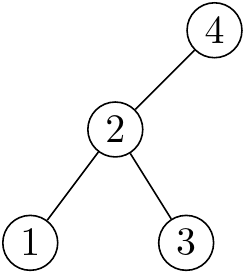
接下來的部份以此類推。可以發現,每一個新的數字都只有一個可以放的位置,而且他一定會跟原本的樹連邊(除了第一個點以外)。所以從前序還原整棵樹的方法,其實就是依序把每一個數字插入到這棵樹上!
這樣的方法行得通,不過我們之前有學過,當二元樹非常不平衡的時候,每一次插入的複雜度會是 $O(N)$。應該要有更快的方法才對……
回顧一下前面的方法,每次增加一個點的時候,我們會有一些可能的「候選位置」。如下圖:
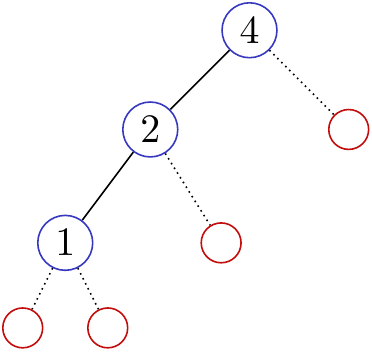
此時我們可以根據新的點的數值,判斷他要放在哪一個侯選位置(紅色圈圈)上。那我們把 $3$ 加進去之後,會有什麼改變呢?
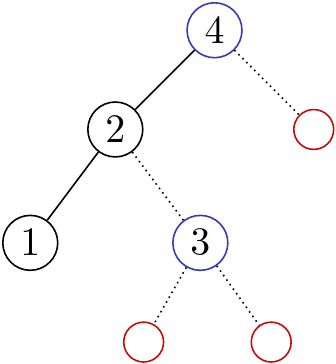
注意到,因為 $3$ 已經接在 $2$ 的右邊了,所以 $2$ 已經處理完他的左子樹中所有的節點,而 $1$ 底下也不會有任何點了!我們可以用藍色的圈圈來表示「後面的數字有可能是他的小孩」的點。接下來我們再把 $5$ 加入到樹中:
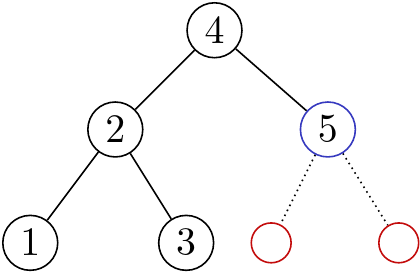
同樣的道理,因為 $5$ 接在 $4$ 的右邊,這就代表 $4$ 的左子樹已經處理完成,因此接下來的點都一定在 $5$ 的底下。因此,我們只需要想辦法維護藍色的點,每次新增的時候選擇某個藍點底下插入,並且更新藍點的集合,就能成功還原這棵樹!
還不是很懂沒關係,直接來看看程式碼:
// 假設有 n 個數字,編號為 1 到 n
int pre[n]; // pre[i] 是前序第 i 項
// 因為我們等一下需要拿倒數第二個東西,所以用 vector 來當作 stack
vector<int> stk;
int lef[n + 1] = {}, rig[n + 1] = {}; // lef[i], rig[i] 是 i 的左、右子節點
for (int i = 0; i < n; i++) {
if (i == 0) { //根節點
stk.push_back(pre[i]);
continue;
}
while ((int)stk.size() >= 2 && pre[i] > stk[(int)stk.size() - 2]){
// pre[i] 不可能是 stk.back() 的小孩
// stk.back() 將來也不會有新的小孩
stk.pop_back();
}
//此時 pre[i] 是 stk.back() 的小孩
if (pre[i] < stk.back()) { // 要放在左邊
lef[stk.back()] = pre[i];
} else { // 要放在右邊
rig[stk.back()] = pre[i];
stk.pop_back(); // stk.back() 以後不會有新的小孩
}
stk.push_back(pre[i]); // pre[i] 加入到藍點
}這個作法運用到一個性質,藍點的數值從上到下的話一定會遞減!為什麼呢?藍點的意義也可以想成是「可能會在右小孩新增節點的人」。因此一個藍點不可能在右邊有小孩,所以下面的藍點一定會更小。同樣的道理,當我們在某個藍點 $x$ 的右邊新增小孩時,$x$ 以及 $x$ 下面的所有點都不會是藍點了,因此我們會把他從 stk 移除。這就表示,藍點之間自然形成了一個堆疊(Stack)的資料結構。
上面的方法同時告訴我們,給定一個二元樹的前序和中序(不一定要是二元搜尋樹),一定能夠還原這棵樹。因為我們可以利用中序遍歷把數字重新編號為 $1$ 到 $n$,然後做一樣的事情。
一個二元樹是一個「樹狀的堆積結構」代表:任何非根節點(non-root node)的值都比其父節點(parent node)的數值還要大。
現在給你某棵「樹狀堆積結構」的中序表示法(in-order),請求出它的前序表示法(pre-order)。
給你一個二元搜尋樹前序遍歷的結果,請你輸出此二元搜尋樹後序遍歷的結果。
條件限制
- $1 \leq N \leq 2000$
- $0 \leq k_i < 10^5$
- 所有節點的值皆相異
相信大家都知道四則運算有一定的順序。而我們其實可以用二元樹的架構來思考要如何表示一個數學式。
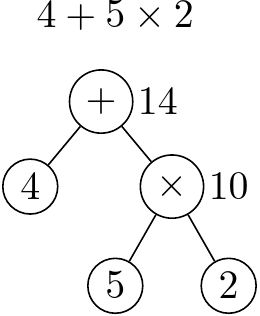
每一個節點的數值就是他的子樹的算式計算的結果。這棵樹的「中序表達式」就是原本的算式:
$$4 + (5 \times 2)$$
如果我們把這個算式的「後序表達式」寫下來的話,那麼會得到 4 5 2 $\times$ $+$。這樣寫的好處是,我們可以輕鬆的從這個後序陣列計算這個算式的答案。
int num[n]; // num[i] 代表第 i 個數字(如果不是運算子的話)
int type[n]; // type[i] == 0 代表是數字, type[i] == 1,2,3,4 代表是運算子 +,-,*,/
stack<int> stk;
for (int i = 0; i < n; i++) {
if (type[i] == 0) {
stk.push(num[i]);
} else {
// 將 Stack 上面兩個數字拿出來,把運算結果放回去
// 注意順序!
int b = stk.top();
stk.pop();
int a = stk.top();
stk.pop();
int result;
if (type[i] == 1) result = a + b;
else if (type[i] == 2) result = a - b;
else if (type[i] == 3) result = a * b;
else result = a / b;
stk.push(result);
}
}所以,我們如果要計算一個算式,首先可以把他轉成後序的形式,再用上面的方法算出。要怎麼轉成後序呢?
首先,算式裡的每一個元素(數字或運算子)都是一個節點,而算式的順序是那棵樹的中序。每個節點會有一個「優先度」,而這個優先度會告訴我們那個點應該放在哪裡。根據四則運算的規則,先被計算的東西應該要放在比較下面的地方(像是上面的圖, $\times$ 被放在 $+$ 的下面)。和前面的概念一樣,如果一個優先度較低的點($+$)出現了,那就代表他會覆蓋掉優先度較高($\times$)的點。因此我們一樣可以維護一個 Stack,裡面存著尚未確定兩邊計算結果的點。
int num[n]; //num[i] 代表第 i 個數字(如果不是運算子的話)
int type[n]; //type[i] == 0 代表是數字, type[i] == 1,2,3,4 代表是運算子 +,-,*,/
//現在的陣列是中序
stack<int> stk;
vector<int> post_num, post_type; //後序的結果
for (int i = 0; i < n; i++) {
if (type[i] == 0) {
//數字優先序最高,直接放到後序
post_num.push_back(num[i]);
post_type.push_back(0);
} else {
//假設 +- 優先度相同, */ 優先度相同,所以從左至右計算
//因為左至右計算,所以寫 <=
while (!stk.empty() && (type[i] - 1) / 2 <= (stk.top() - 1) / 2) {
//把 stack pop 掉
post_type.push_back(stk.top());
post_num.push_back(0);
stk.pop();
}
stk.push(type[i]);
}
}
while (!stk.empty()) { //還在 stack 的人依序清空
post_type.push_back(stk.top());
post_num.push_back(0);
stk.pop();
}給定某個包含 +, -, *, /, () 的算式,請求出計算的結果。
Hint: 想想看括號的情形要怎麼辦!