堆積（Heap） 是一個相對簡單的樹狀資料結構。他的實作概念是基於二元樹，而樹上的每一個節點儲存一個可以比較大小的鍵值（key），並支援以下操作：

• 插入一個鍵值
• 詢問目前最大的鍵值
• 刪除最大的鍵值

堆積會根據根節點的值是最小或最大值分為最小堆（Min-Heap）和最大堆（Max-Heap）。對於一個 Min-Heap，一個節點的值一定比其子樹的每一個節點的值都小，對於一個 Max-Heap，則是都大。還有一個重要的性質就是：通常實作的時候會把這個樹當成一個完全二元樹（也就是除了最後一階可能不填滿其他都滿）的樹，這個好處就是可以用陣列存這個樹。

Tips 1

用陣列存二元樹

給定一個陣列，可以用陣列來存二元樹，節點由上到下，由左到右一層層編號：

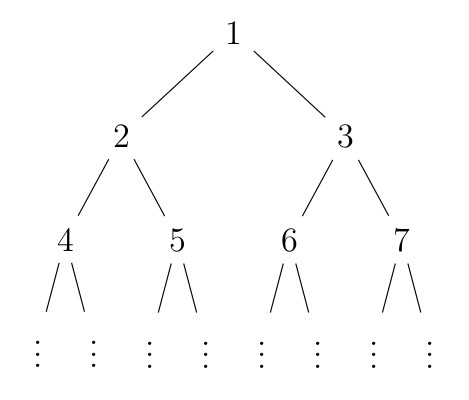
經觀察可以發現：編號為 $i$ 的節點左節點為 $2i$，右節點為 $2i + 1$，而其父節點為 $\lfloor \frac{i}{2} \rfloor$。如果是完全二元樹，就可以發現只需要 $O(n)$ 的空間來存；但是如果退化成鏈可就糟糕了：需要 $O(2^n)$ 的空間存，所以這種儲存方法最適合用在高度不高（像是 $O(\log n)$）的樹，而 Heap 正好符合這個性質。

顯然，對於一個數字的集合，也會有許多的 Min(Max) Heap 可能。以下所講的 Heap 皆指 Min-Heap，至於 Max-Heap 的實作就只是把不等號反過來就好了。另外，以下所說的「最後的節點」指的是最後一層最右邊的節點。

要支援的操作比較多，讓我們一個個拿出來討論。這邊我們用 vector 做為一種陣列的實作。

• int getMin()，代表回傳堆疊根節點的值（也就是最小值），複雜度 $O(1)$。

  int getMin(vector<int> &heap) {
      if (heap.empty())
          printf("empty!\n");
      else return heap[1];
  }

• void insert(int x)
  要加入一個值為 $x$ 的數字進去 Heap 裡面。作法就是先將 $x$ 先丟進去最下面，然後一直往上，只要發現 $x$ 現在的節點比其父節點的值小，就交換他們兩個，並繼續看。

  void Insert(vector<int> &heap, int x) {
      heap.push_back(x);
      int last = heap.size() - 1;
      while (last > 1){
          if (heap[last] < heap[last / 2])
              swap(heap[last], heap[last / 2]);
          last /= 2;
      }
  }

• void deleteRoot(int x)
  刪除根節點。將根換成最後的節點（最後的節點也刪掉），然後開始遞迴往下：如果目前的值比左右子樹的最小值大，則與左右子樹的最小值交換，並且往那個子樹遞迴下去。

  void deleteRoot(vector<int> &heap) {
      swap(heap[1], heap[heap.size() - 1]);
      heap.pop_back();
      int pos = 1;
      while (pos < heap.size()) {
          int l = 2 * pos, r = 2 * pos + 1;
          if (l >= heap.size()) break;
          int min_child = r;
          if (r >= heap.size() || heap[l] < heap[r])
              min_child = l;
          if (heap[min_child] < heap[pos]) {
              swap(heap[pos], heap[min_child]);
              pos = min_child;
          }
          else break;
      }
  }

不難發現，insert() 和 deleteRoot() 的複雜度都是 $O(\log n)$，因為最差就是一直遞迴到底，而因為是完全二元樹，就有 $O(\log n)$ 層。

當然，超棒的 STL 有提供 Heap 可以用，稱為 priority_queue，但是不一定是依照以上的實作。

我們可以用下列方法宣告一個 priority_queue：

priority_queue<int> pq; // 宣告一個整數的 max-heap
 

不過就好比排序，我們有時候會想要自定義排序基準，在 priority_queue 我們也會想要定義誰是「最大值」。若要自行定義比較函數（也就是定義「小於」），可以下列方式進行：

priority_queue<int, vector<int>, greater<int> > min_pq;
// 把「小於」定義成「大於」，也就是 min-heap
priority_queue<int, vector<int>, comp> custom_pq; 
// 自訂義小於比較

priority_queue 的比較函數稍微複雜一點，要用 struct 的 operator() 來實作，以下是實作方法：

struct comp {
    bool operator()(int a,int b) {
        return a % 10 < b % 10;
    }
};

上述 comp 放進 priority_queue 之後，製造出來的效果會是維護「數字的末位數最大的值」。

STL 內建的 priority_queue 一樣支援了 heap 該有的操作：

• push() 可以將資料丟入堆積的內部；
• pop() 將最大元素刪除；
• top() 查詢堆積內的最大元素；
• size() 查詢堆積的資料數；
• empty() 回傳堆積是否為空。

pq.push(3);
pq.push(2);
cout << pq.top() << endl; // 3
pq.pop();
cout << pq.top() << endl; // 2

Heap 可以運用在非常多的題目內，不過那是未來篇章的事情了。這裡就先放上一些基本的操作題：