在一般的陣列裡面,每個東西會放在一個有編號的格子裡。但如果我們想要在陣列中間插入某個東西,或是把一段陣列平移到別的地方的話,可能會需要更有彈性的資料結構。此時,Linked List 就是一個合適的選擇。
現在假設我們在玩一個遊戲:每一個人都要指一個人,那要怎麼紀錄這種關係呢?將每一個人想成一個東西,裡面包著自己的值和指向的人!這就是 Linked List 的精神。如下圖:

這裡,蕭梓宏指向王政祺,王政祺指向林尚廷……直到劉至軒停止。用資訊的術語來講,每一個東西稱作一個節點(node)。
有時候,會有人想要知道是誰指向自己,就會再維護一個指標指向「指向自己的那個人」,圖形大概長這樣:

作法就是:當 A 連到 B 的時候,將 A 指向的人設為 B,而 B 的被指的人設為 A。
了解作法之後,就來看看如何實作吧!
請你實做一個 linked-list ,並實現以下指令:
1 n:將整數 $n$ 放進 linked-list 的頭2 n:將整數 $n$ 放進 linked-list 的尾3 n a:將整數 $n$ 放到整數 $a$ 的前面,若 $a$ 不存在則印出peko並略過這個操作4 n a:將整數 $n$ 放到整數 $a$ 的後面,若 $a$ 不存在則印出peko並略過這個操作5 a:印出整數 $a$ 前面的整數,若此整數不存在則印出NULL,若 $a$ 不存在則印出peko6 a:印出整數 $a$ 後面的整數,若此整數不存在則印出NULL,若 $a$ 不存在則印出peko7 a:刪除整數 $a$,若 $a$ 不存在則印出peko並略過這個操作
條件限制
- 保證所有操作
1,2,3,4中的整數 $n$ 不會重複 - $指令數 \leq 20000$
- $0 < $ 所有整數 $\leq 100000$
讓我們一步步看要怎麼支援每個操作:
首先,我們假設每個節點可以直接用他的編號讀取,並把所需要存取的資料宣告成陣列,再寫好一個初始化用的函式:
int prev_node[maxn]; // 上一個節點編號
int next_node[maxn]; // 下一個節點編號
int is_inserted[maxn]; // 節點是否在 linked list 裡面
// 初始化節點 x
void Init(int x, int prv, int nxt, int inserted) {
prev_node[x] = prv;
next_node[x] = nxt;
is_inserted[x] = inserted;
}其中 prev_node 和 next_node 就是這個節點指向的前一個/後一個人。但如果前一項或後一項不存在時怎麼辦?這裡我們可以使用一個聰明的小技巧,可以發現題目並不會用到 $0$ 這個編號,所以不如就把 $0$ 當作不存在的象徵。
同時,我們還可以刻意讓陣列中 $0$ 的位置存上有關於頭尾的資訊,讀者也可以想像成我們把 linked list 變成這種樣子:
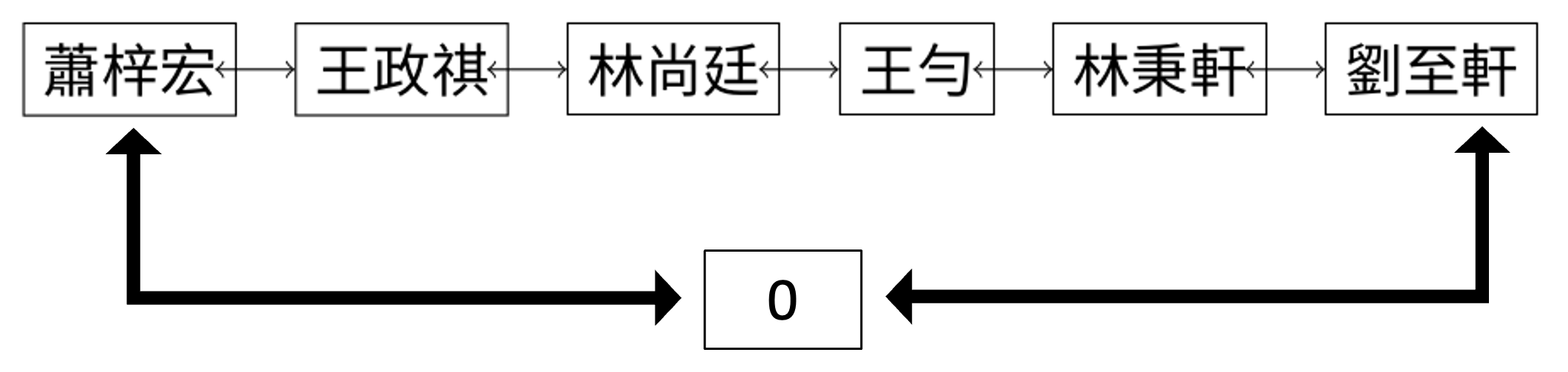
也就是製造一個假想節點在頭尾!這樣就可以省下不少方便的判斷了,讀者可以透過後面的實作來感受其簡潔性。
// 刻意使用一點小聰明,讓節點編號 0 同時當作頭尾
Init(0, 0, 0, 1);接下來讓我們看看插入操作的細節。當我們要在節點 $a$ 後插入一個點 $n$ 時,原本 $a$ 跟 $a$ 的下一項中間的連結會被斷開,然後我們要把中間的連跟這兩個點各自連接。
// 在節點 x 之後插入 id 的節點
void Insert(int x, int id) {
int nxt = next_node[x];
Init(id, x, nxt, 1);
prev_node[nxt] = id;
next_node[x] = id;
}刪除也是類似,就是變成反過來把 $a$ 的前一項和下一項連結回來。
// 刪除節點 x
void Delete(int x) {
int prv = prev_node[x];
int nxt = next_node[x];
is_inserted[x] = 0;
next_node[prv] = nxt;
prev_node[nxt] = prv;
}至於要怎麼在節點 $a$ 前面插入節點呢?這裡不用再重新實作一個新的函式,可以直接想成是「在節點 $a$ 的上一個節點」後面插入節點!類似的想法也可以套用到插入頭尾的操作,只要好好思考假想節點 $0$ 的概念就好。
以下附上完整的實作,讀者可以多加反思:
#include <iostream>
using namespace std;
const int maxn = 100005;
int prev_node[maxn]; // 上一個節點編號
int next_node[maxn]; // 下一個節點編號
int is_inserted[maxn]; // 節點是否在 linked list 裡面
// 初始化節點 x
void Init(int x, int prv, int nxt, int inserted) {
prev_node[x] = prv;
next_node[x] = nxt;
is_inserted[x] = inserted;
}
// 在節點 x 之後插入 id 的節點
void Insert(int x, int id) {
int nxt = next_node[x];
Init(id, x, nxt, 1);
prev_node[nxt] = id;
next_node[x] = id;
}
// 刪除節點 x
void Delete(int x) {
int prv = prev_node[x];
int nxt = next_node[x];
is_inserted[x] = 0;
next_node[prv] = nxt;
prev_node[nxt] = prv;
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
// 刻意使用一點小聰明,讓節點編號 0 同時當作頭尾
Init(0, 0, 0, 1);
int m;
cin >> m;
while (m--) {
int op;
cin >> op;
if (op == 1) {
int n;
cin >> n;
Insert(0, n);
}
else if (op == 2) {
int n;
cin >> n;
Insert(prev_node[0], n);
}
else if (op == 3) {
int n, a;
cin >> n >> a;
if (!is_inserted[a])
cout << "peko\n";
else
Insert(prev_node[a], n);
}
else if (op == 4) {
int n, a;
cin >> n >> a;
if (!is_inserted[a])
cout << "peko\n";
else
Insert(a, n);
}
else if (op == 5) {
int a;
cin >> a;
if (!is_inserted[a])
cout << "peko\n";
else if (prev_node[a] == 0)
cout << "NULL\n";
else
cout << prev_node[a] << "\n";
}
else if (op == 6) {
int a;
cin >> a;
if (!is_inserted[a])
cout << "peko\n";
else if (next_node[a] == 0)
cout << "NULL\n";
else
cout << next_node[a] << "\n";
}
else if (op == 7) {
int a;
cin >> a;
if (!is_inserted[a])
cout << "peko\n";
else
Delete(a);
}
}
}
Linked list 的使用時機:
當題目出現「在某個位置插入/刪除元素」,或者是把一段區間的元素移動/反轉的操作,可能就是 Linked List 出場的時間。
STL 也為 linked list 設計了一個容器適配器,不過由於 linked list 的操作較為複雜,有許多操作需要跟Iterator有一定的熟悉度,建議讀者先有基本的認知再閱讀這個小節。以下是 list 的宣告方法。
list<int> lst; // // 宣告一個儲存 int 型別的 list
list 是放在 <list> 標頭檔內,使用前記得引入。
push_back()可以將資料放入list尾端;pop_back()將list尾端的元素刪除push_front()可以將資料放入list前端;pop_front()將list前端的元素刪除front()查詢list前端元素back()查詢list後端元素insert()可以插入元素在一個list內的iterator的前方;size()查詢目前還位於list的資料數;empty()回傳list是否為空。splice()可以在 $O(1)$ 時間內將一個list串接另一個list的任何位置
list<int> lsta, lstb;
lsta.push_back(3); // a: [3], b: []
lsta.push_back(1); // a: [3, 1], b: []
lsta.push_front(2); // a: [2, 3, 1], b: []
lsta.pop_back(); // a: [2, 3], b: []
lsta.pop_front(); // a: [3], b: []
lsta.push_front(1); // a: [1, 3], b: []
lstb.push_front(4); // a: [1, 3], b: [4]
lstb.push_back(5); // a: [1, 3], b: [4, 5]
lsta.splice(next(lsta.begin()), lstb); // a: [1, 4, 5, 3], b: []
cout << lsta.front() << endl; // 1
cout << lsta.back() << endl; // 3
cout << lstb.size() << endl; // 0
不過這樣似乎衍伸了一些問題:
在 STL list 的世界中,存取單一節點資訊除了頭尾外,幾乎都是使用該節點的 iterator 來進行存取,在拿到 iteartor 後,就可以呼叫 iterator 的通用函式 prev() 和 next() 來獲得資料。而若要獲得一個 list 的頭尾節點本身,使用 begin() 和 --end() 即可。
這裡就需要使用一些慣用手法,一種常見的做法便是「儲存節點的 iterator」,直接宣告一個陣列來儲存每個節點在 list 內的位置,這樣就可以直接戳出想要的位置了!
下面這份程式碼使用 STL 實作出了前面的例題,讀者可以比對著研究看看。
#include <iostream>
#include <list>
using namespace std;
const int maxn = 100005;
// 用來紀錄每個節點對應在 lst 內的位置
list<int>::iterator node_it[maxn];
int main() {
ios::sync_with_stdio(0), cin.tie(0);
list<int> lst;
// 在所有節點都尚未插入的情況下,初始化每個節點的位置為不存在的 lst.end()
for (int i = 0; i < maxn; ++i)
node_it[i] = lst.end();
int m;
cin >> m;
while (m--) {
int op;
cin >> op;
if (op == 1) {
int n;
cin >> n;
lst.push_front(n);
node_it[n] = lst.begin();
}
else if (op == 2) {
int n;
cin >> n;
lst.push_back(n);
node_it[n] = --lst.end();
}
else if (op == 3) {
int n, a;
cin >> n >> a;
if (node_it[a] == lst.end())
cout << "peko\n";
else
node_it[n] = lst.insert(node_it[a], n);
}
else if (op == 4) {
int n, a;
cin >> n >> a;
if (node_it[a] == lst.end())
cout << "peko\n";
else
node_it[n] = lst.insert(next(node_it[a]), n);
}
else if (op == 5) {
int a;
cin >> a;
if (node_it[a] == lst.end())
cout << "peko\n";
else if (prev(node_it[a]) == lst.end())
cout << "NULL\n";
else
cout << *prev(node_it[a]) << "\n";
}
else if (op == 6) {
int a;
cin >> a;
if (node_it[a] == lst.end())
cout << "peko\n";
else if (next(node_it[a]) == lst.end())
cout << "NULL\n";
else
cout << *next(node_it[a]) << "\n";
}
else if (op == 7) {
int a;
cin >> a;
if (node_it[a] == lst.end())
cout << "peko\n";
else {
lst.erase(node_it[a]);
node_it[a] = lst.end();
}
}
}
}
再讓我們來看看一道應用題:
輸入說明
第一行包含一個整數 $N$,代表現在有 $N$ 個玩家,編號 $1\sim N$ 的玩家目前分別為第 $1\sim N$ 名(編號 $1$ 第 $1$ 名、編號 $2$ 第 $2$ 名……)。
第二行包含一個整數 $M$,代表接下來會依序發生 $M$ 個事件。
接下來的 $M$ 行,每行包含兩個整數 $T_i,X_i$,$T_i$ 為 $0$ 的時候,代表編號 $X_i$ 的玩家遭受攻擊,然後離開遊戲;$T_i$ 為 $1$ 的時候,代表編號 $X_i$ 的玩家使用衝刺,無條件超越當前名次比他高一名的玩家。
輸出說明
輸出一行,包含 $Y$ 個整數($Y$ 是剩餘玩家的數量),由名次小到大依序輸出,整數兩兩間以空白隔開。
條件限制
- $N\leq 10^5$
- $M\leq 50000$
- $0\leq T_i\leq 1$
- $1\leq X_i\leq N$
- 測試資料保證玩家被淘汰之後不會再出現任何紀錄。
對於初始序列的建構,轉化成按照名次順序插入節點就行了。刪除節點的操作,模板就有直接支援。超越的部分比較麻煩,對於每一筆超越的操作,可以想像成先將前一名的節點刪除,再插入到自己的後面,因為 Linked List 對於 id 的插入、刪除操作都是 $O(1)$ ,所以總複雜度 $O(N+M)$。
以下這份程式碼繼承了我們最一開始的 linked list 實作,讀者有興趣也可以自行使用 STL 的 list 實作看看:
int main() {
ios::sync_with_stdio(0), cin.tie(0);
Init(0, 0, 0, 1);
int n, m;
cin >> n >> m;
// 初始化
for (int i = 0; i < n; ++i)
Insert(i, i + 1);
while (m--) {
int op, id;
cin >> op >> id;
if (op == 0) {
// 刪除節點 id
Delete(id);
}
else {
// 超越前一名
int p = prev_node[id];
if (p != 0) {
int pp = prev_node[p];
Delete(p);
Delete(id);
Insert(pp, id);
Insert(id, p);
}
}
}
// 遍歷整個 list
int cur = next_node[0];
while (cur != 0) {
cout << cur << " \n"[next_node[cur] == 0];
cur = next_node[cur];
}
}如果想要查詢「一個東西指到誰?」的話,顯然這個可以在 $O(1)$ 內做完。那如果想要做的是查詢「我這個人一直指,指到第 $k$ 個人會是誰呢?」那就得花 $O(k)$ 的時間,所以 Linked List 不適合隨機存取,也就是在只給串列頭的狀況下,查詢第 $n$ 項的值,會變得很慢。
注意到,這樣代表 Linked List 跟陣列有點像是相反的資料結構。Linked List 可以在 $O(1)$ 時間插入/刪除元素,但是需要 $O(n)$ 時間從頭開始找某一項。陣列則是要花 $O(n)$ 時間插入跟刪除元素,不過在 $O(1)$ 時間就能找到某一項。
$n$ 個人站成一列,請執行 $m$ 次操作,每次都會把編號 $k$ 後面的人殺掉,並輸出這個被殺掉的人的編號。
條件限制
- $1\leq n, m\leq 10^6$
有 $N$ 個店家在販賣物品,顧客們想在任何店家買東西都需要排隊,請支援 $M$ 筆操作:
ADD$\;i\;id$:代表編號為 $id$ 的顧客前往店家 $i$,排在隊伍的最後端LEAVE$\;i$:代表店家 $i$ 賣出了一個物品給排在隊伍最前端的顧客,該顧客會離開隊伍JOIN$\;i\;j$:店家 $i$ 的物品賣完了,所以排在店家 $i$ 的隊伍會按照順序重新排在店家j的後面
條件限制
- $N\leq 100$
- $M\leq 10^5$
- 顧客編號介在 $1\sim 10^6$ 之間
- 保證同一個顧客不會同時出現在不同隊伍中。