讓我們來看看下面這道題目：

我們先來「設計狀態」，若貿然的令 $dp[i]$ 是考慮第 $i$ 天結束的最大快樂值總和時，就會發現一個嚴重的問題──我們在轉移的時候不知道如何判斷是否連續兩天做了一樣的活動！

左想右想，把狀態敘述得再清楚好像都解決不了這個問題，那該怎麼辦呢？

其實，我們在設計狀態的時候可以不要拘泥於「一個 dp 式」，俗話說的好，一個不夠那就用兩個，如果還不夠──那就用三個。

我們就宣告三個 dp 式：$dpa[i], dpb[i], dpc[i]$，分別代表

• $dpa[i]$ 是經過了前 $i$ 天，且第 $i$ 天選擇了活動 A 的最大快樂值總和。
• $dpb[i]$ 是經過了前 $i$ 天，且第 $i$ 天選擇了活動 B 的最大快樂值總和。
• $dpc[i]$ 是經過了前 $i$ 天，且第 $i$ 天選擇了活動 C 的最大快樂值總和。

那如何寫出轉移式呢？當然是互相轉移囉！拿 $dpa$ 做為舉例：

$$
dpa[i] = \max(dpb[i - 1] + a_i, dpc[i - 1] + a_i)
$$

沒錯，因為如果第 $i$ 天選擇了活動 A，那麼唯一的限制就是第 $i-1$ 天不可以有活動 A。因此，有了 $dpb$ 和 $dpc$ 的幫助，我們就可以某種程度上「指定」第 $i-1$ 天的活動，來迴避連續兩天做一樣活動的狀況。

附上程式碼供參考

#include <iostream>
#include <algorithm>
using namespace std;

const int MAXN = 100005;

int a[MAXN], b[MAXN], c[MAXN];
int dpa[MAXN], dpb[MAXN], dpc[MAXN];

int main() {
    ios::sync_with_stdio(0), cin.tie(0);
    int n;
    cin >> n;
    for (int i = 1; i <= n; ++i) 
        cin >> a[i] >> b[i] >> c[i];
    for (int i = 1; i <= n; ++i) {
        dpa[i] = max(dpb[i - 1] + a[i], dpc[i - 1] + a[i]);
        dpb[i] = max(dpc[i - 1] + b[i], dpa[i - 1] + b[i]);
        dpc[i] = max(dpa[i - 1] + c[i], dpb[i - 1] + c[i]);
    }
    cout << max({dpa[n], dpb[n], dpc[n]}) << "\n";
}

在前一個章節，我們提到設計動態規劃演算法的第一步是「設計狀態」，但我們好像一口氣就設計了不只一種狀態，這樣真的合理嗎？其實我們不妨用這種方式去想：

• $dp[i][j]$ 是經過了前 $i$ 天，且第 $i$ 天選擇了第 $j$ 種活動的最大快樂值總和。
  • 這裡的 $j=0, 1, 2$ 分別就對應到活動 A, B, C。

沒錯！就是直接把 dp 狀態想成「二維」的就好了。還記得我們在介紹「狀態」這個用語時有提到，其實 dp 的狀態是用少少的幾個參數定義出來的，因此當然不會永遠都只有一個 $i$ 囉。

甚至用這種方式去實作的話，就可以把程式碼再寫得美一些：

#include <iostream>
#include <algorithm>
using namespace std;

const int MAXN = 100005;

int happiness[MAXN][3];
int dp[MAXN][3];

int main() {
    ios::sync_with_stdio(0), cin.tie(0);
    int n;
    cin >> n;
    for (int i = 1; i <= n; ++i) 
        for (int j = 0; j < 3; ++j)
            cin >> happiness[i][j];
    for (int i = 1; i <= n; ++i) {
        for (int j = 0; j < 3; ++j)
            for (int k = 0; k < 3; ++k)
                if (j != k)
                    dp[i][j] = max(dp[i][j], dp[i - 1][k] + happiness[i][j]);
    }
    cout << *max_element(dp[n], dp[n] + 3) << "\n";
}

雖然比起之前的程式碼長，但陣列的版本看起來不會有一堆長得一樣的片段。這樣的好處除了可以輕鬆應付「當活動種類數變多」的狀況外，若 dp 轉移式變得複雜，當我們不小心寫錯時，要進行修改就不用每行都改一遍了。

讓我們來重新複習一下這題：

在前一個章節，我們的做法是先定義好狀態之後，試著整理轉移式才能將時間複雜度優化至 $O(N)$。有沒有直接一點的 $O(N)$ 做法呢？

這時候我們就能利用「增加維度」的方式，來直接的辦到這件事！

我們定義兩種狀態，$dp[i][0]$ 和 $dp[i][1]$：

• $dp[i][0]$ 代表到了第 $i$ 天結束後，手上沒有持有股票的最大獲利
• $dp[i][1]$ 代表到了第 $i$ 天結束後，手上持有股票的最大獲利

這樣轉移該如何運作呢？

針對 $dp[i][0]$，前一天會有兩種可能：要嘛前一天也沒有股票，要嘛前一天還有股票。因此，對於這兩種狀況，我們就能依序寫出 $dp[i - 1][0]$ 和 $dp[i - 1][1]$ 的子問題，其中因為後者還要「賣股票」，所以要多加上 $a_i$，寫出來就是
$$
dp[i][0] = \max(dp[i - 1][0], dp[i - 1][1] + a_i)
$$

而對 $dp[i][1]$，前一天會有兩種可能：要嘛前一天也有股票，要嘛前一天沒有股票。這裡的概念也差不多，但對於後者，要多注意多等 $1$ 天的問題，所以要取 $dp[i - 2][0]$ 這個子問題，寫出來就是
$$
dp[i][1] = \max(dp[i - 1][1], dp[i - 2][0] - a_i)
$$

讀者可以想成是我們在模擬第 $i$ 天當下「可能做出的決策」。還記得我們說動態規劃的狀態就是在「描繪出答案被構建出來的過程」，而轉移就是在「描述過程之間是如何轉換的」：

• 在前一個章節的做法中，我們是在把買賣股票「每一組買賣」都當成一種過程的變化，也因此，每一次轉移跨越的天數就會是 $O(N)$ 級別的。
• 在現在的做法裡，我們是在把「每一天的決定」當成一種過程的變化，而一天的決定通常只取決於前一天或前兩天的結果，所以每一次轉移跨越的天數就會是 $O(1)$。

上述是筆者針對這兩種做法的解釋，並沒有唯一的解釋方法，讀者在這部分的意義上可以自行多加思考看看，相信可以對這樣子的變化有多一層的理解。

當然，這兩種做法並沒有絕對是誰好誰壞的問題，總是有題目可以讓其中一種做法有明顯的優勢在。因此很多時候在解題時，我們會需要多方嘗試各種不同的狀態設計，並思考相應的轉移意義，才能找到解出題目的正確方向。

附上程式碼給讀者自行比對：

#include <iostream>
using namespace std;

const int MAXN = 100005;

int arr[MAXN], dp[MAXN][2];

int main() {
    ios::sync_with_stdio(0), cin.tie(0);
    int n;
    cin >> n;
    for (int i = 1; i <= n; ++i)
        cin >> arr[i];
    const int INF = 1e9;
    dp[0][1] = -INF;
    dp[1][0] = 0;
    dp[1][1] = -arr[1];
    for (int i = 2; i <= n; ++i) {
        dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + arr[i]);
        dp[i][1] = max(dp[i - 1][1], dp[i - 2][0] - arr[i]);
    }
    cout << dp[n][0] << "\n";
}

相信讀者對這道問題並不陌生，其實這就是在問我們高中學習的組合數問題，也就是 $C^n_m$。

當然，若讀者熟悉基礎數學 / 基礎數論中提到的模逆元的話，就會知道對於每一組 $n, m$ 的詢問，都可以在經過 $O(n)$ 的預處理後以 $O(1)$ 時間內回答任何一組詢問。但若題目要求的模數不是質數，或甚至當 $n, m$ 比模數還大時，就會出現問題。

因此，我們可以利用組合數的遞迴性質，也就是：

$$
C^n_m = C^{n-1}_m + C^{n-1}_{m-1}
$$

這個式子又被稱為巴斯卡恆等式，要直觀解釋的話，可以想成 $n$ 個元素選出 $m$ 個的方法可以來自：

• 拿第 $n$ 個元素，因此剩下對應到一個「$n-1$ 個元素、選 $m-1$ 個」的子問題。
• 不拿第 $n$ 個元素，因此剩下對應到一個「$n-1$ 個元素、選 $m$ 個」的子問題。

因此，取這兩種「狀態」的總和，就可以直接得到上面的「轉移式」。

#include <iostream>
using namespace std;

const int MOD = 1e9 + 7;
const int MAXN = 1005;

int C[MAXN][MAXN];

int main() {
    ios::sync_with_stdio(0), cin.tie(0);
    C[0][0] = 1;
    for (int i = 1; i < MAXN; ++i) {
        C[i][0] = 1;
        for (int j = 1; j <= i; ++j)
            C[i][j] = (C[i - 1][j] + C[i - 1][j - 1]) % MOD;
    }
    int q;
    cin >> q;
    while (q--) {
        int n, m;
        cin >> n >> m;
        cout << C[n][m] << "\n";
    }
}

將其實作成程式碼，讀者就可以發現我們在過程中只有用到加法，也因此對於任意的模數都不成問題！

看完數方法數的例子，我們就來看看最佳化問題的例子。

最長共同子序列（Longest Common Subsequence，簡稱 LCS）是一個非常經典的 dp 例題。但在定義狀態之前，我們應該來分析一下這道問題答案的結構是如何。

所謂「子序列」，就可以想成一組索引值序列 $i_1\leq i_2\leq \cdots\leq i_k$，而兩個字串的「共同子序列」即代表著，有另一組一樣長的索引值序列 $j_1\leq j_2\leq \cdots\leq j_k$，滿足

$$
\text{對於所有 }t\text{，}A_{i_t}=B_{j_t}
$$

想到這裡，一種狀態的定義就出現了：$dp[i][j]$ 即代表著「結尾是 $A_i$ 和 $B_j$ 的最長共同子序列長度」，而轉移只要窮舉上一次的結尾在哪就好了，也就是說：

$$
dp[i][j] =
\begin{cases}
0 & i = j = 0 \\
-\infty & A_i\neq B_j\text{，字元不同不能當結尾} \\
\max_{a<i, b<j} dp[a][b] + 1 & A_i=B_j\text{，窮舉上一個字元的位置}
\end{cases}
$$

不過仔細分析看看時間複雜度，若令 $N=|A|$、$M=|B|$，$O(NM)$ 的狀態搭配 $O(NM)$ 的轉移，整體的時間複雜度居然是 $O((NM)^2)$ 這麼慢！

這裡就需要用到一點狀態設計的巧思，若我們巧妙的修改一下狀態定義——$dp[i][j]$ 代表著「字串 $A$ 長度為 $i$ 的前綴、與字串 $B$ 長度為 $j$ 的前綴，兩者的最長共同子序列長度」。

這樣帶來的好處是什麼呢？讀者可以想像是我們將前面的狀態做了某種二維前綴最大值的處理，這讓 $\max_{a<i, b<j}dp[a][b] + 1$ 的這個複雜的轉移，瞬間變成了一個 $dp[i - 1][j - 1] + 1$ 的 $O(1)$ 轉移！

整理一下轉移式，我們可以得到
$$
dp[i][j] =
\begin{cases}
0 & i = 0 \text{ 或 } j = 0 \\
\max\{dp[i - 1][j], dp[i][j - 1]\} & A_i\neq B_j\text{，只維護二維前綴的極值} \\
\max\{dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1] + 1\} & A_i=B_j\text{，額外考慮接一個字元在後面} \\
\end{cases}
$$

但其實從上式中我們可以觀察到，$i$ 跟 $j$ 多增加 $1$ 時，$dp[i][j]$ 的值其實也只會提升頂多 $1$ 而已。因此，這個轉移式可以簡化成
$$
dp[i][j] =
\begin{cases}
0 & i = 0 \text{ 或 } j = 0 \\
\max\{dp[i - 1][j], dp[i][j - 1]\} & A_i\neq B_j\text{，只維護二維前綴的極值} \\
dp[i - 1][j - 1] + 1 & A_i=B_j\text{，額外考慮接一個字元在後面} \\
\end{cases}
$$

就得到一個 $O(NM)$ 的動態規劃演算法了。

#include <iostream>
#include <string>
using namespace std;

const int MAXN = 5005;
int dp[MAXN][MAXN];

int main() {
    ios::sync_with_stdio(0), cin.tie(0);
    string a, b;
    cin >> a >> b;
    int n = a.size(), m = b.size();

    // 插入首字元使兩字串變成 1-base
    a.insert(a.begin(), '?');
    b.insert(b.begin(), '!');

    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= m; ++j)
            if (a[i] != b[j])
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
            else 
                dp[i][j] = dp[i - 1][j - 1] + 1;
    cout << dp[n][m] << "\n";
}

當然，狀態的維度可不僅限於二維而已，就讓我們看看下面這道例題：

這題是進化版的 LCS 問題，而作法當然也就跟前面非常相似，具體來說，只要令 $dp[i][j][k]$ 是三個字串中長度分別為 $i, j, k$ 的前綴的最佳答案，就可以依樣畫葫蘆寫出類似的轉移式。由於非常相似，接下來的部份就交給讀者了。

總而言之，讀者可千萬不要被狀態中「參數的個數」所限制住，只要我們需要的資訊量不足，就得考慮是否要增加維度來「保持我們需要的資訊」的狀態上，才能寫出相對應的轉移式。

在本節中，我們帶讀者了解到在設計動態規劃演算法時，很多時候僅僅靠一個參數是無法準確的維護狀態轉移的過程的，也因此我們才需要狀態維度的增加。而透過上述幾道例題，相信讀者也體認到了增加狀態的效益、以及其必要性。

當然，讀者可能會發現在本節中出現的例題都有著較為單純的狀態定義。因此，在接下來的章節中，我們將在讀者對維度的擴增有一定的熟悉度的前提下，帶讀者認識一些較為不直觀的幾種典型狀態設計方法。

多了「增加狀態」這個武器後，能解的動態規劃問題一下子就變多了！因此我們準備了豐富的習題，就讓讀者好好練習囉！

-1 7 -8 10 -5
-4 -9 8 -6 0
5 -2 -6 -6 7
-7 4 7 -3 -3
7 1 -6 4 -9

習題

Chest of Drawers

Source:UVa 11420

斗櫃就是如左圖由很多抽屜垂直排列組成的櫃子。雖然這是個很有用的家具，但是如果要鎖這些抽屜時卻發生了問題——抽屜即使上鎖了也不一定安全。例如假設從上面往下數第三個抽屜鎖上了，但是它上面的那個抽屜卻沒鎖。這時鎖起來的抽屜也不安全，因為只要把它上面的抽屜整個拉出來就可拿到裡面的東西了。

一個 $n$ 個抽屜的斗櫃，會有數個方式來確保剛好有 $s$ 個抽屜是安全的。以左圖的斗櫃為例，有六個方式可以確保剛好四個抽屜是安全的。這六個方式如下圖所示。

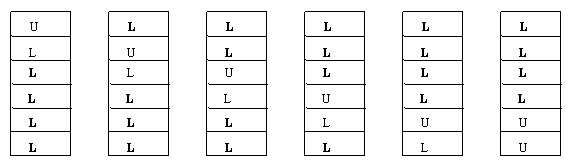
圖中的 L 表示那個抽屜是鎖著的，U 則表示沒上鎖。這就是可以確保剛好 4 個抽屜是安全的的六個組合。安全的抽屜以粗體字母來表示。

給你 $n$ 和 $s$ 的值，請你算有多少個方式可以確保它們的安全。

條件限制

• 最多 $5000$ 筆測資
• $1\leq n\leq 65$
• $0\leq s\leq 65$