就讓我們直接來看看這道問題：

方法數要怎麼數呢？一個最直覺的想法就是直接窮舉看看，例如：

• 先爬一階，接下來還有幾種爬法？
• 先爬兩階，接下來還有幾種爬法？

假設這兩種情況的答案都算好了，相加起來就可以直接得到答案。再多看幾眼，爬一階之後還有幾種爬法，不就是爬 $N-1$ 階的方法數嗎？爬兩階也同理。

在學過遞迴之後，應該就可以輕鬆的寫出以下這段程式碼：

long long cal_ans(int n) {
    if (n <= 1) return 1; // base case
    long long ans = 0;
    ans += cal_ans(n - 1); // 先爬一階
    ans += cal_ans(n - 2); // 先爬兩階
    return ans;  
}

然而快樂傳上去的結果就是獲得一坨 TLE，甚至光本地測範測三就跑不完了。可以想像因為我們在 $N$ 的時候就窮舉了兩種情況、$N-1$ 也窮舉兩種情況……這樣下去執行的時間會是指數等級的成長！

這時候就要善用動態規劃的概念——用記憶換取時間，假設我們想要計算出爬 $86$ 階的方法數，那只要先記下爬 $85$ 階、和 $84$ 階的方法數，不就可以 $O(1)$ 得到答案了嗎？同理，要怎麼記下 $85$ 階的方法數呢？只要先記下爬 $84$ 階、和 $83$ 階的方法數就可以了……依此類推。

咦？怎麼感覺到頭來還是每個值都要計算一遍，這樣真的有優化到嗎？優化得可多了，畢竟要記住一件事情之前，你總還是要知道過答案一次，但動態規劃與暴力法不同的是，我們算過一次就不要再算了，也就是計算完畢的當下我們直接把他記起來！

舉例來說，若要算爬 $5$ 階的方法數，暴力法的流程可能如下：

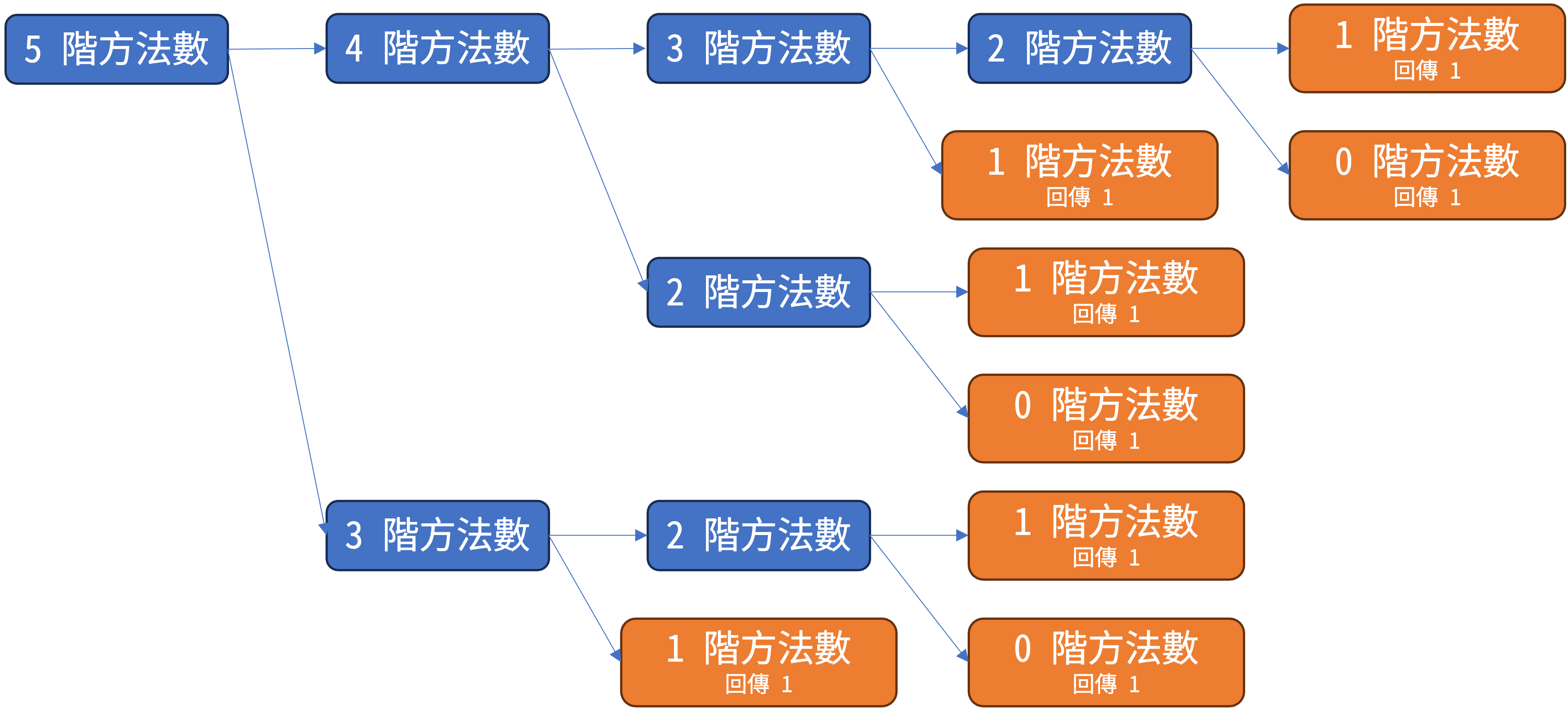
總共就需要花費 $15$ 次呼叫，但如果運用動態規劃的概念呢？

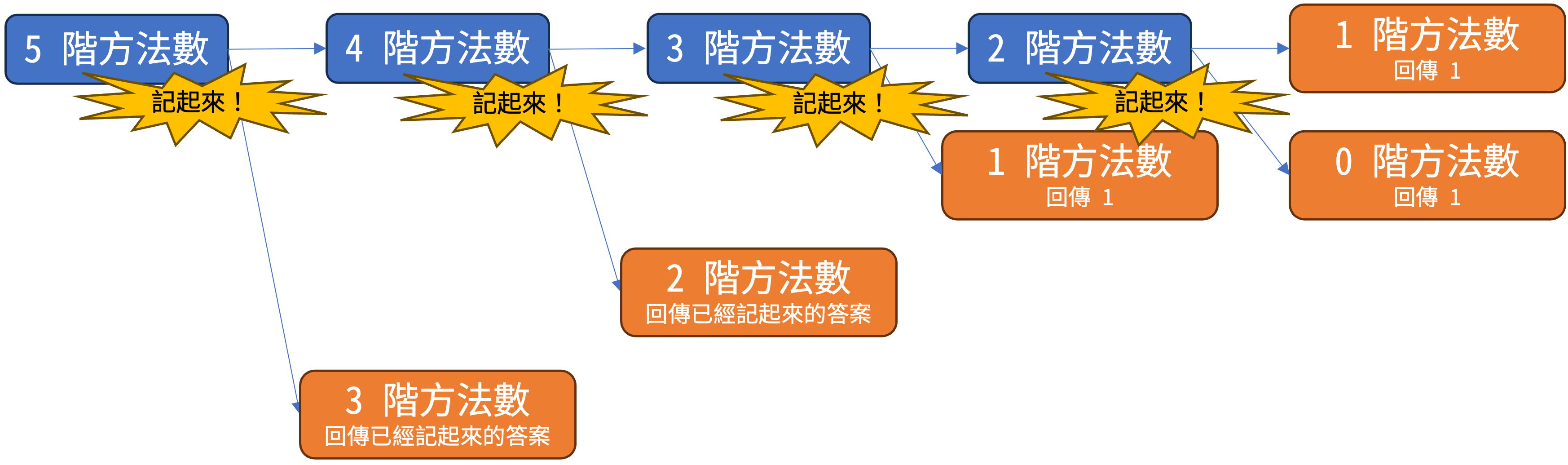
就只剩下 $9$ 次呼叫，雖然看起來好像沒省多少，但隨著 $N$ 變大，省下來的呼叫次數可是非常可觀的。

但具體來說到底變多快呢？詳細一點分析看看：

• 只有 $2\sim N$ 這麼多種答案是我們不知道的。
• 每種答案都只計算一次。
• 每種答案的計算都是花 $O(1)$ 來得知答案。

因此我們得出了結論：使用動態規劃後的時間複雜度是 $O(N)$，比原先指數級的時間複雜度好非常多！

別緊張，要記下答案的人可不是你，可是電腦，因此我們可以直接開一個夠長的陣列來存下答案。寫成程式碼大概就是下列這種樣子：

bool visited[87]; // 是否已經記起來
long long dp[87];

long long cal_ans(int n) {
    if (n <= 1) return 1; // base case
    if (visited[n] == 1) return dp[n]; // 已經記起來了，直接回傳
    visited[n] = 1;
    dp[n] = 0;
    dp[n] += cal_ans(n - 1); // 先爬一階
    dp[n] += cal_ans(n - 2); // 先爬兩階
    return dp[n];
}

是不是意外的單純呢？

順帶一提，如果把爬 $n$ 階的答案寫成一個數列，會得到 $1, 1, 2, 3, 5, 8, \ldots$ 這樣的東西，這個序列又被稱為費氏數列，在組合數學上是一個非常經典的數列。

透過前面的引導，我們來討論在動態規劃中一個相當重要的概念——子問題。

在使用動態規劃處理一個問題時，到底是哪些記憶才能有效的幫忙加速演算法呢？沒錯，其實大多是那些形式與原問題相同、但規模更小的「子問題」。

• 在處理回家問題時，我們記著的是「從學校回家」這個同樣是詢問從指定地點走回家的子問題。
• 在處理爬樓梯問題時，我們要回答爬了 $n$ 階的方法數，也是同樣只把規模更小的 $n-1$ 階、$n-2$ 階、……、直到 $1$ 階的方法數記起來。

也因此，在動態規劃的問題中，熟記以下流程是非常重要的：

用另一個角度想，其實上述在做的事情就跟設計多數遞迴函式是相同的，只是我們多了一道技巧，那就是透過記憶來加速了整個遞迴所花的時間。這也是動態規劃與一般遞迴最大的差別——同樣的子問題，會被呼叫非常多次，進而提高「記憶」的幫助效果。這樣的關鍵差別，我們在演算法中稱之為「重複子問題」。

如果沒有重複子問題的話，既然每個子問題都只會被呼叫一次，又何必需要記憶呢？

在思考動態規劃的問題時，時常需要記憶的子問題是顯然的，但卻常常拿著一些已經記好子問題不知如何湊出真正問題的答案。該怎麼解決呢？很可惜，這通常沒有一個制式化的訣竅，唯有多練習題目才是正道。因此，這裡就帶大家從最基本的動態規劃題型開始了解——也就是我們的線性遞迴函數。

所謂線性遞迴函數呢，最簡單的形式就是要計算目標函數 $f(n)$，並且 $f(n)$ 的值會由「一些較小的項乘上某些倍數後」總和得出。以前面學到的爬樓梯問題為例，當我們把爬 $n$ 階的方法數寫成 $f(n)$ 時，可以得出 $f(n) = f(n - 1) + f(n - 2)$ 這個式子，這樣一個計算的式子又被稱為「遞迴式」。讓我們看看更多例子：

以下幾種遞迴式是線性遞迴：

• $f(n) = 2f(n - 1) + f(n - 2)$
• $f(n) = f(n - 1) - f(n - 3) + 87f(n - 5)$

以下幾種遞迴式則不是線性遞迴：

• $f(n) = f(n - 1)^2$
• $f(n) = f\left(\left\lceil \frac{n}{5}\right\rceil\right) + f\left(\left\lceil \frac{7n}{10}\right\rceil\right) + c\cdot n$

不過，光是寫出遞迴式其實並不能夠完整呈述一個遞迴函數，有一個必要的要素常被忽略、卻是不可或缺的——那就是「基底」，也常被稱作 base case。實際上，爬樓梯問題的遞迴函數要寫完整的一點的話應該寫成如下：

$$
f(n) =
\begin{cases}
1 & n \leq 1 \\
f(n - 1) + f(n - 2) & \text{otherwise}
\end{cases}
$$

在上述式子中，我們把所謂「最簡單的子問題」寫進去了，而這就是一個遞迴函數需要具備的基底。由於基底通常是容易得出的，因此時常我們在敘述、甚至設計演算法時都會省略基底的敘述，但寫程式時可千萬不能忽略這樣的小細節。

當然，線性遞迴函數在數學上還有更廣泛的定義，但不在我們這次的討論範圍中，讀者只需要先簡單知道以上的形式就可以了。接下來，我們就來用兩道線性遞迴的題目試試身手：

例題

Brick Wall Patterns

Source:ZeroJudge d038

如果我們要用常見的長度為高度兩倍的磚塊建一道磚牆，並且牆的高度為兩個單位，根據牆的長度，我們可以建出不同數量的花樣。從下圖我們可以看出：

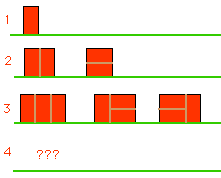
• 長度為 1 單位的牆只有一種花樣—就是讓磚塊直立。
• 長度為 2 的牆有 2 種花樣—兩個平躺的磚磈疊在一起以及兩個直立的磚塊併在一起。
• 長度為 3 的牆有三種花樣。

長度為 4 的牆你可以找出幾種花樣？那長度為 5 的牆呢？

你的工作是要寫一個程式，給它牆的長度（$n$），它就算出這道牆可以有幾種花樣。

條件限制

• $1\leq n \leq 50$

若要找出需要記憶的子問題，想必只能是記下所有「長度為 $n$ 的牆」的擺放方法數了。但數擺放方法數的題目要怎麼利用子問題呢？通常，我們會想像這些磚塊是「由左擺放至右的」，也因此，「最後擺了什麼」可能就可以成為找出利用子問題的關鍵。

若我們嘗試畫出長度為 $4$ 的牆：

好像能發現，我們總是可以在盡量右邊切下一刀，並把左右邊分開來：

更進一步的，只要看到能夠切開的地方就切開的話：

也因此，這個「擺放」的流程，就可以想成是不斷擺上互相能夠切開的小磚牆，而經過仔細思考之後就會發現：

• 當不能切開的長度是 $1$ 時，肯定只有把磚塊直著放一種可能。
• 當不能切開的長度是 $2$ 時，肯定只有把兩個磚塊橫著放一種可能。
• 當長度超過 $2$ 時，肯定有一個地方是可以切開的。

沒錯，這告訴了我們擺放長度為 $n$ 的牆可以看成：

• 擺放不能切開的長度 $1$ 磚牆在後面，得到長度為 $n-1$ 的牆的子問題。
• 擺放不能切開的長度 $2$ 磚牆在後面，得到長度為 $n-2$ 的牆的子問題。

兩個方法的總和。

因此，其實這道問題與爬樓梯問題一樣，都是費氏數列，開心的修改輸入格式之後傳上去獲得 AC 吧！

例題

DELIVERY DEBACLE

Source:ZeroJudge d054

Wolfgang Puck 有兩個很特別的習慣：

• 他只做兩種形狀的蛋糕。一種是面積為一單位的方形，另一種是面積為三單位的 L 形。

• 他只用特定尺寸的盒子來裝蛋糕。這些盒子的寛度都是二單位，但各種不同長度都有。

有一天，Wolfgang 想知道有幾種不同的方式可以把蛋糕裝滿一個特定尺寸（$2\times n$）的盒子。你能幫他嗎？

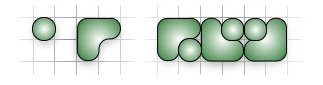
上圖中，左圖為蛋糕的尺寸，右圖為裝滿長度 $6$ 的盒子的一種方法。

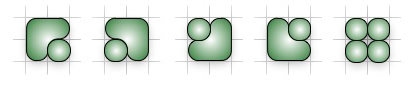
上圖則是裝滿長度為 $2$ 的盒子的所有方法，共有 $5$ 種。

條件限制

• $1\leq n \leq 40$

風格很像的題目，不過這次可不再是費氏數列了！但不怕，我們用類似的思路下去思考這題。

一樣，試著畫出長度夠短時的狀況，從題目給的圖片我們似乎可以得出：

• 當不能切開的長度是 $1$ 時，肯定只有直著放兩顆方形蛋糕一種可能。
• 當不能切開的長度是 $2$ 時，肯定是由一個 L 形 + 一個方形組成，旋轉後共有四種可能。
• 當長度超過 $2$ 時，肯定有一個地方是可以切開的。

因此，該題的遞迴式便呼之欲出：$f(n) = f(n - 1) + 4f(n - 2)$。但如果就這樣快樂的寫出以下這段程式碼：

long long cal_ans(int n) {
    if (n <= 1) return 1;
    if (visited[n] == 1) return dp[n];
    visited[n] = 1;
    dp[n] = 0;
    dp[n] += cal_ans(n - 1);
    dp[n] += 4 * cal_ans(n - 2);
    return dp[n];
}

居然就拿到 Wrong Answer！

多想一下，其實我們還漏了一種狀況：

• 當不能切開的長度是 $3$ 時，肯定是由兩個 L 形上下對接組成，翻轉後共有兩種可能。

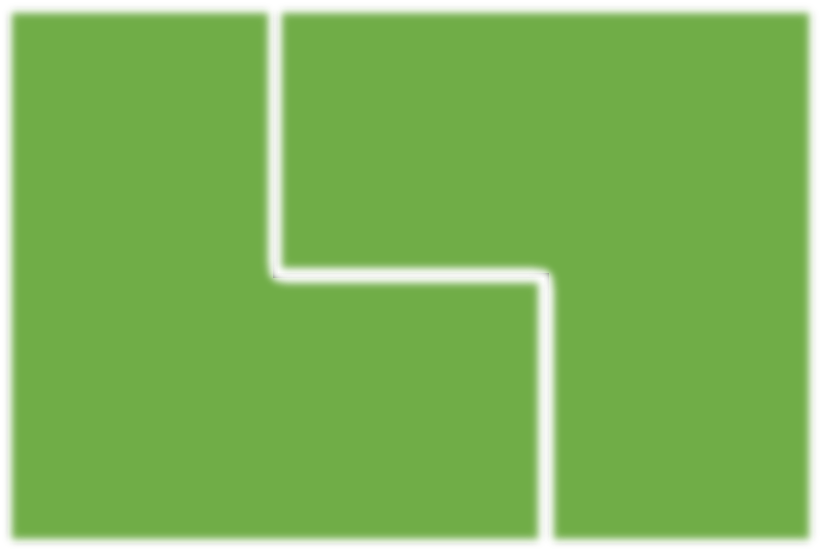
沒錯，其實這題要當長度超過 $3$ 時，才肯定有一個地方是可以切開的。也就是說遞迴式實際上是 $f(n) = f(n - 1) + 4f(n - 2) + 2f(n - 3)$，我們得多補一行

    dp[n] += 2 * cal_ans(n - 3);

才可以正確……先等等，這樣可是會 WA 的，還記得前面我們才強調過遞迴的「基底」很容易被忽略嗎？沒錯，在這裡，要注意到當 $n=2$ 時會不小心呼叫到 cal_ans(-1) 造成問題！這裡可以簡單的在前面補上一行

    if (n == 2) return 5;

就能答對這題了。

讓我們順便複習一下這題完整的遞迴函數形式：

$$
f(n) =
\begin{cases}
1 & n \leq 1 \\
5 & n = 2 \\
f(n - 1) + 4f(n - 2) + 2f(n - 3) & \text{otherwise}
\end{cases}
$$

不過話又說回來，為什麼會發生漏了一種狀況的情況呢？殘忍一點地說，這其實沒有什麼通則，反而比較像是一種「細心程度」的檢驗。從上面的題目中我們可以學到，當在處理「找到使用子問題湊出答案的方法」時，我們是需要考慮好所有可能性的！這需要多花一點心思來檢驗自己有沒有漏掉任何情況，只能說解題時要多加小心囉！

在這個章節中，我們簡單了解了在解決動態規劃問題時最基礎的概念、以及需要注意的事項。

我們知道在設計動態規劃的演算法時，最重要的就是找到有效的「重複子問題」，並透過思考和經驗來嘗試找到如何用子問題得到完整問題的答案。

了解完子問題後，我們學習到了線性遞迴的一般解題思路與需要注意的細節；而在下一個章節，我們會先繼續圍繞在線性遞迴上，來讓大家透過已經熟悉的線性遞迴問題了解處理動態規劃問題時在競賽程式中不可或缺的常識。

習題

會議中心（Room）

Source:TIOJ 1476

拼拼樂會議中心是一個 $N\times N$ 的超大型可分割式會議中心。

每一個 $1\times 1$ 的空間都可以用隔板隔開，因此該會議中心最多可以有 $n^2$ 個獨立的 $1\times 1$ 會議室，如要較大的會議室，則需將隔板拿掉使得二或更多個相鄰的 $1\times 1$ 空間可以合併使用。

每間 $1\times 1$ 會議室皆以其二維平面座標為編號。選定一個 $1\times 1$ 會議室並給予編號 $(0,0)$，相鄰的上、下、左、右會議室編號則依序為 $(0, 1), (0, -1), (-1, 0), (0, 1)$。會議中心外租會議室時，必須按照下列規則，組成合乎需求的會議室。一開始先以編號為 $(0, 0)$ 的空間供租用，如果空間不足，則依序向右方、上方、左方、下方的空間合併成為較大的會議室。

每次擴充時，新加入的空間必須為正方形且該邊長必須與相鄰的擴充前會議室邊長相同，如此才能確保合併後的會議室一定是四方形。

以下圖為例，第一次擴充租用空間時，右邊編號為 $(1, 0)$ 的會議室空間會被跟編號為 $(0,0)$ 的會議室合併。

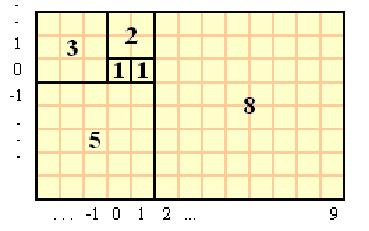
第二次擴充時，在 $(0, 0), (1, 0)$ 上方的四個（$2\times 2$ 正方形）小會議室會被合併進來。

第三次擴充時，在 $(0,0) \sim (0, 3)$ 左邊的 $9$ 個（$3\times 3$ 正方形）小會議室會被合併進來。

第四次擴充時，在 $(-3,0) \sim (1,0)$ 下方的 $25$ 個（$5\times 5$ 正方形）小會議室會被合併進來。

第五次擴充時，在 $(0,-5) \sim (0,2)$ 右方的 $64$ 個（$8\times 8$ 正方形）小會議室會被合併進來。後續的擴充則依此類推。

現在，若給定一個 $n$ 的值，請計算第 $n$ 次擴充時的正方形會議室的邊長。

條件限制

• $n\leq 45$

習題

A Graph Problem

Source:ZeroJudge d389

給一個有 $n$ 個節點的無向圖形（圖形如下

你的任務是：給你 $n$，請算出這個圖形有以下性質的節點子集合共有多少個。

集合裡不能有兩個相鄰的點。例如圖形中有 $n=3$ 個節點，則集合 $\{1,2\}$ 是違法的，而集合 $\{1,3\}$ 是合法的。
當這個集合能再加入任一節點，卻可以不和其它節點相鄰，則這個集合是違法的。例如圖形中有 $n=5$ 個節點，則集合 $\{1,5\}$ 是違法的，因為這個集合再加入節點 $3$ 仍不和其它節點相鄰，而集合 $\{1,3,5\}$ 則是合法的。
所以，當圖形有 $n=5$ 個節點時，應該有 $4$ 個合法的集合：$\{1,3,5\},\{2,4\},\{2,5\},\{1,4\}$。

條件限制

• 輸入至 EOF 結束
• $1\leq n\leq 76$