讓我們直接來檢驗一下大家在上一個章節學到的線性遞迴：

假設我們要計算 $n$ 個人的解，我們只要試圖窮舉站在第 $n$ 個人左邊的人是誰，不就得到一個子問題了嗎？這裡我們就廢話不多說，直接寫出完整的遞迴式：

$$
f(n) =
\begin{cases}
1 & n = 1 \\
1 & n = 2 \\
f(n - 1) + f(n - 2) & \text{otherwise}
\end{cases}
$$

原來又是費式數列啊！正當我們興高采烈的貼上我們熟悉的費氏數列程式碼、小改一下基底執行後，卻意識到了哪裡不對勁──我們必須輸出方法數除以 $10^9 + 7$ 的餘數？

直接算出 $f(n)$ 之後再使用 % 運算子是不行的，光是在 $n=93$ 時，這題的答案就會正式超出 long long int 可以儲存的範圍，那用大數運算呢？恐怕也不行，費氏數列的成長速度是非常快的，很可能還碰不到 $n=10^5$ 就會因為位數太多造成 TLE。

所以該怎麼辦呢？這裡就要提到一個數學小技巧──先取餘數再進行運算、和先運算後再取餘數，得到的結果其實是一樣的！

（更詳細的數學原理，可以參考基礎數學 / 常用數學演算法）

也就是說，我們可以在計算完一個 dp 值時，直接將其變成除以 $10^9 + 7$ 的餘數，再進行後續的運算，如下列程式碼所寫的：

const int MOD = 1000000007;

int cal_dp(int n) {
    if (n == 1) return 1;
    if (n == 2) return 1;
    if (visited[n] == 1) return dp[n];
    visited[n] = 1;
    dp[n] = (cal_dp(n - 1) + cal_dp(n - 2)) % MOD;
    return dp[n];
}

太好了，解決了取餘數的問題後看起來沒問題了，正當我們這麼想時在本地測試了一下最大的範例測資 $n=10^7$ 時，本地卻出現了疑似 RE 的錯誤！

這樣的程式怎麼會出錯呢？若嘗試不信邪的傳到 Online Judge 上，竟然可以發現他神奇 AC 了，到底是什麼詭異的理由導致了這樣的結果？

實際上，我們在本地遭遇的問題是程式中一個經典的問題──「stack overflow」。若讀者已經先讀過章節實作知識 / 全域、區域變數相信就知道這裡在講什麼了。但白話一點說的話，就是一般在程式設計中，函式呼叫所使用到的空間是較沒有防護措施的，也因此在執行程式時為了安全性作業系統通常都會預設一個較小的上限值，這時候使用一個遞迴太多層──我們稱做「遞迴過深」──的函式時，就會踩到這個上限值導致 RE。為了避免這個問題，Online Judge 通常會特別把這個上限值調大，才不會在 Judge 上吃 RE，但本地可沒有做任何處理，這也是為什麼會發生這樣的差異。

雖然好像傳上去就會過了，可是如果本地都沒辦法好好測試的話就麻煩了，當然，雖然我們可以試圖調大上限值來解決這個問題，但能不能不要仰賴過深的遞迴解決這個問題呢？

遞迴過深的問題可不只有會遇到上限值不夠的 Online Judge 而已，在「演算法常數」的部分，遞迴所製造的常數往往都比非遞迴來得大，尤其在動態規劃的題目中，我們常常都會用另一種非遞迴方法來實作一個動態規劃的演算法──我們稱之為 Bottom up。

Bottom up 顧名思義就是希望「從底下算上來」；而相對起來，我們之前教的遞迴實作方法則是被稱作「Top down」。拿費式數列當例子，當我們要計算 $f(4)$ 時，使用 Top down 的感覺是這樣的：

• 呼叫 $f(4)$ $\xrightarrow{\text{發現 }f(3)\text{ 和 }f(2)\text{ 都還沒計算過 }}$ 呼叫 $f(3)$ 和 $f(2)$ $\rightarrow$ $\ldots$ $\xrightarrow{\text{等待子問題計算完畢}}$ 算出 $f(4)$

這個「發現還沒計算過」的步驟其實有點多餘，如果我們事先把 $f(3)$ 和 $f(2)$ 都算好，不就可以一步直接提取 $f(3)$ 和 $f(2)$ 的值加總起來了嗎？

因此，Bottom up 的核心就是「試圖從最基礎的 case 一路算上來」，例如上述計算出 $f(4)$ 的過程就是

• 已知 $f(0)$ 和 $f(1)$ $\xrightarrow{\text{直接得到值計算總和}}$ 算出 $f(2)$ $\xrightarrow{\text{直接得到值計算總和}}$ 算出 $f(3)$ $\xrightarrow{\text{直接得到值計算總和}}$ 算出 $f(4)$

那 Bottom up 寫成程式碼之後又會如何呢？其實非常乾淨：

const int MOD = 1000000007;

int cal_dp(int n) {
    dp[1] = dp[2] = 1;
    for (int i = 3; i <= n; ++i)
        dp[i] = (dp[i - 1] + dp[i - 2]) % MOD;
    return dp[n];
}

沒錯，一個迴圈就能解決所有！不僅解決了遞迴過深造成的問題，連寫法上都簡單不少，有沒有覺得 Bottom up 優點非常多呢？

讓我們再來看看下面這道例題：

老樣子，我們一樣在計算 $n$ 個人的解時，窮舉站在第 $n$ 個人左邊的人是誰就可以得到一個子問題。但第 $n$ 個人左邊的人可以是誰？可以是第 $n-2$ 個人、第 $n-3$ 個人、……、到第 $1$ 個人都有可能！

因此，如果列出遞迴式，會是這樣的：

$$
f(n) =
\begin{cases}
1 & n = 1 \\
0 & n = 2 \\
\sum_{i=1}^{n-2} f(i) & \text{otherwise}
\end{cases}
$$

可以發現，為了計算「總和」，我們在計算出一個 $f(n)$ 的值時，會需要花費的時間是 $O(n)$ 的，寫成 Bottom up 的程式碼的話可能會更加明確：

const int MOD = 998244353;

int cal_dp(int n) {
    dp[1] = 1, dp[2] = 0;
    for (int i = 3; i <= n; ++i) {
        dp[i] = 0;
        for (int j = 1; j <= i - 2; ++j)
            dp[i] = (dp[i] + dp[j]) % MOD;
    }
    return dp[n];
}

很明顯，總共的時間複雜度就是 $O(n^2)$，這是肯定會超時的！

要怎麼進一步優化時間複雜度呢？仔細觀察一下就可以發現，當我們計算完 dp[i - 1] 的值後 dp[i] 所要計算的值其實差不了多少：

• dp[i - 1]：計算從 dp[1] 到 dp[i - 3] 的總和
• dp[i]：計算從 dp[1] 到 dp[i - 2] 的總和

兩者的差距只有在 dp[i] 的時候多了一個 dp[i - 2] 而已！

既然他們要計算的總和差異這麼小，我們不妨多開一個變數紀錄當前的總和，在計算新的一個 dp 值時，把差異補上去就好了，具體寫起來如下：

const int MOD = 998244353;

int cal_dp(int n) {
    int sum = 0;
    dp[1] = 1, dp[2] = 0;
    for (int i = 3; i <= n; ++i) {
        sum = (sum + dp[i - 2]) % MOD;
        dp[i] = sum;
    }
    return dp[n];
}

程式碼裡面的 sum 變數就是在紀錄該次 dp 值算完時的總和，我們只要透過這個變數的輔助，就能「省下」那些重複的計算，進而把每次計算 dp 值的時間優化至 $O(1)$！

這同時也是 Bottom up 的優勢之一，在 Top down 的實作裡，若要這樣實作，我們得額外開的就是一個 sum 陣列，用來儲存「每個 dp 值計算完時的 sum 值」，會變得麻煩一些。

這題比前面的題目都還要複雜一些，為何這麼說呢？如果我們直接採用前面的老方法的話：

• 首先定義 $g(n)$ 是當集合的最後一個數字是 $n$ 時的方法數
  • 也就是說，$f(n) = \sum^n_{i=1} g(i)$
• 計算 $g(n)$ 時，窮舉集合內倒數第二個數字是誰……

卡住了，那三個連續正整數到底應該出現在哪呢？

我們先別急著換一個方向思考，來檢討一下現在這個老方法產生的問題：

• 在先前的題目中，我們總是仰賴著最後一個區塊的長相來寫出遞迴式
  • 在 Brick Wall Patterns 中，我們找到最後一小塊不能切開的小磚牆
  • 在 別離太遠/別離太近 中，我們找到最後一個人
• 有了最後一個區塊之後，我們知道更前面的區塊答案恰好是子問題的答案
  • 在 Brick Wall Patterns 中，拿走最後一小塊不能切開的小磚牆，就是一個更小的子問題
  • 在 別離太遠/別離太近 中，拿走最後一個人，就是一個更小的子問題

所以不妨思考看看：計算 $g(n)$ 拿走了集合內的 $n$ 時，假設倒數第二個數字是 $i$ 好了，這真的是一個更小的子問題、$g(i)$ 嗎？答案是不對的！

考慮以下這個會被算進去 $g(5)$ 的集合

$$
\{1, 3, 4, 5\}
$$

當我們拿走了 $5$，會得到 $\{1, 3, 4\}$，這可不是 $g(4)$ 會算到的東西，這也就造成我們的老方法行不通了。

那該怎麼辦呢？是時候動點手腳了！既然我們不太擅長計算「存在三個連續正整數」的集合個數，不如來算算「不存在三個連續正整數」的集合個數。

這樣有什麼用呢？非常有用！因為：

• 所有的集合很好算：有 $n$ 個數字，每個數字取或不取，因此總共有 $2^n$ 種集合
• 「存在三個連續正整數的集合個數」，就是「所有的集合個數」扣掉「不存在三個連續正整數的集合個數」

所以我們就能來專心算「不存在三個連續正整數」的集合個數了！這裡我們重新將 $f(n)$ 定義成 $1\sim n$ 中不存在三個連續正整數的集合個數，這時候再套用我們的老方法：

• 首先定義 $g(n)$ 是當集合的最後一個數字是 $n$ 時的方法數
  • 也就是說，$f(n) = \sum^n_{i=1} g(i)$
• 計算 $g(n)$ 時，最後一段連續的數字可以是
  • $n$：這時候再前一個數字不會是 $n-1$，因此根據前一個數字是多少，可以接上子問題 $g(n-2), g(n-3), \ldots, g(0)$
  • $n - 1, n$：這時候再前一個數字不會是 $n-2$，因此根據前一個數字是多少，可以接上子問題 $g(n-3), g(n-4), \ldots, g(0)$
  • 再多就出現連續三個數字了！
• 因此可以寫出遞迴式

$$
g(n) =
\begin{cases}
1 & n = 0 \\
1 & n = 1 \\
2 & n = 2 \\
\sum^{n-2}_{i=0} g(i) + \sum^{n-3}_{i=0} g(i) & \text{otherwise}
\end{cases}
$$

這時候就又能使用我們前一道題目學會的技巧了，也就是開一個變數紀錄當前要用到的總和，這裡開兩個變數稍微麻煩了一些，我們不妨將第四種情況改寫成

$$
\left(g(n - 2) + \sum^{n-3}_{i=0} g(i)\right) + \sum^{n-3}_{i=0} g(i)
$$

就可以共用同一個總和了！寫成程式碼之後如下：

const int MOD = 1e9 + 7;
const int MAXN = 1000000;

int dp[MAXN + 5];

void cal_dp(int n) {
    int sum = 0;
    dp[0] = 1, dp[1] = 1, dp[2] = 2;
    for (int i = 3; i <= n; ++i) {
        sum = (sum + dp[i - 3]) % MOD;
        dp[i] = ((dp[i - 2] + sum) + sum) % MOD;
    }
}

再來就是要計算真正的答案了，注意到題目會做 $t$ 次詢問，因為 $t\leq 10$ 每次重跑一次 cal_dp 後當然可以通過，但為了幫助讀者未來遇到 $t \leq 10^6$ 這種量級的詢問量時，還是順便在這裡提醒讀者可以預處理答案，因此我們在這裡實作一個函式 build_ans 來蓋出所有 $n$ 介在 $1\sim 10^6$ 的答案：

int ans[MAXN + 5];

void build_ans(int n) {
    cal_dp(n);
    int power2 = 1, sum = dp[0];
    ans[0] = 0;
    for (int i = 1; i <= n; ++i) {
        sum = (sum + dp[i]) % MOD; // 當前的「不存在三個連續正整數」集合個數
        power2 = power2 * 2 % MOD; // 順便維護當前的子集合個數
        ans[i] = (power2 - sum) % MOD;
    }
}

好了，既然都寫好程式碼了就來補上 main 函式，

int main() {
    ios::sync_with_stdio(0), cin.tie(0);
    build_ans(MAXN); // 一口氣把 1000000 以內的答案都算好
    int t;
    cin >> t;
    while (t--) {
        int n;
        cin >> n;
        cout << ans[n] << "\n";
    }
}

再來上傳看看……居然只答對了第一子題！？

其實這裡還踩到了一些常見的小陷阱，這裡我們就帶讀者來看看問題是什麼，比賽的時候可千萬要小心。

讓我們看看前面程式碼片段中的這行：

        dp[i] = ((dp[i - 2] + sum) + sum) % MOD;

在這裡，我們連續把三個 int 型態的整數加了起來，但每一個數字最大可以是多少呢？是 $10^9+7-1$！三個 $10^9$ 附近的數字相加是肯定會超過 int 範圍上限的。

這樣的問題該如何解決呢？一個很簡單的方式就是將所有變數改成 long long 型態，但為此動輒所有變數實在是太麻煩了。

這裡，我們可以在運算過程中將變數「轉型」，也就是先暫時將數字變成使用 long long 做運算，運算出的結果用 long long 存著後，再透過最後的 % MOD 讓數字變回 int！

講起來複雜，但實際上只需要這樣寫就搞定了：

        dp[i] = ((long long)(dp[i - 2] + sum) + sum) % MOD;

邏輯上，會需要想著「運算的順序」。而上面式子的運算順序就是先進行括號內 dp[i - 2] + sum 的運算後，被前方的 (long long) 轉型成 long long 型態，再和 int 型態的 sum 做運算，而在 C++ 中，long long 和 int 同時做運算時，int 會被強制轉型成 long long，也因此整個式子就能在 long long 的庇護下避免溢位了。

不過既然 long long 和 int 同時做運算時，int 會被強制轉型成 long long，這裡就存在第二種簡潔的寫法：

        dp[i] = (0ll + (dp[i - 2] + sum) + sum) % MOD;

我們一樣試著思考運算的順序，在同樣的先算好括號內 dp[i - 2] + sum 的運算後，由於加法運算子是由左至右運算，因此左方的 0ll + 會在接下來被運算，這時候，寫成 0ll 的常數 0 是被強制指定成 long long 型態的，因此在這瞬間，後方 (dp[i - 2] + sum) 的運算結果也在這時候從 int 被轉型成了 long long！接下來的運算也就跟原本一樣了。

為何運算順序如此重要呢？一個例子就好比下面這段改造失敗的程式碼，讀者可以自行思考看看其發生錯誤的原因：

        dp[i] = ((dp[i - 2] + sum) + sum + 0ll) % MOD;

不過上述的問題修正完成後並沒有讓我們直接通過此題，這是因為還有另一處問題，讓我們看看下面這行程式碼：

        ans[i] = (power2 - sum) % MOD;

實作技巧 / 常見錯誤列表中，小節「負數取模」有提到負數取模之後只要沒整除就還會是負數，因此在上述這行式子內，很有可能 ans[i] 的值會得到一個負數。

要解決這個問題，照著先前提到的解決方法多寫下一行 ans[i] = (ans[i] % MOD + MOD) % MOD 當然可以，但根據狀況其實有這樣簡單的解決方法：

        ans[i] = (power2 + MOD - sum) % MOD;

這是因為 sum 的絕對值肯定小於 MOD，也因此單獨看後方的 MOD - sum 肯定會是正值，而兩個 $10^9$ 附近的數字相加又不會 overflow，所以乾淨的多加一個 MOD 就能解決問題。

不過這樣的技巧有時候不見得管用，所以讀者務必要多熟悉運算順序以及他們可能的值來評估問題是否可能會發生。若嫌麻煩的話，還有一個懶人招數就是直接不管那麼多，就算是負數也照存不誤，只要在最後在 main 裡輸出答案時再轉回正數就可以了。

在這個章節中，我們了解了 Bottom up 的動態規劃實作方式，並體會到了不少使用我們原先學習的 Top down 作法無法獲得的優勢，其中包含了：

• 避免遞迴過深
• 擁有較小的演算法常數
• 能夠較為直接的用來進行演算法優化
  • 例如直接在 Bottom up 的過程中多開一個變數來紀錄我們想利用的「總和」

但特別提醒讀者，Top down 可不是完全沒有用，在往後較為進階的章節，我們會再把它拿出來講，可別忘記它的存在了。

除了學習到 Bottom up 之外，我們還多順便學會了一些線性遞迴變化題的解題方法和思路，但動態規劃可不只是如此！因此，在下一個章節，我們會開始帶讀者認識一些不再是單純線性遞迴的問題，並藉此帶大家認識我們在設計動態規劃演算法時更一般的邏輯來加深概念。

習題

鋪磁磚問題

Source:北市賽 2005 pC

某學校有一片狹長形狀的畸零地，其寬度、長度分別為 $30$ 公分及 $n\times 10$ 公分，但在西北角缺了寬度、長度均為 $10$ 公分的一角。現在我們要使用 $\frac{3\times n - 1}{2}$ 塊磁磚將此片畸零地鋪滿，每塊磁磚的寬度、長度均為 $10$ 公分及 $20$ 公分，我們想知道共有多少種鋪法。請你撰寫一個程式來求出答案。以下圖為例，當 $n=3$ 時，可看出共有 $4$ 種不同的鋪法。

當 $n=5$ 時，由下圖，可看出共有 $15$ 種不同的鋪法。

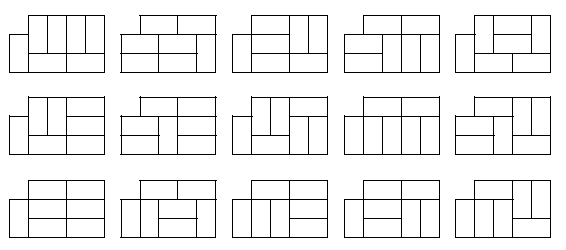
條件限制

• 輸入到 EOF 為止
• $n$ 為奇數，$3\leq n\leq 41$

習題

網路建設 (Fibers)

Source:全國賽 2016 pB

抓寶網路公司正在幫和平社區規劃新一代的網路架構，該社區的網路平面架構圖如下，其中有編號的頂點代表網路設備的位置，兩個相鄰頂點之間有一虛線段連接，線段部分代表可以鋪設網路光纖的路線，網路設備可以透過光纖連結起來。

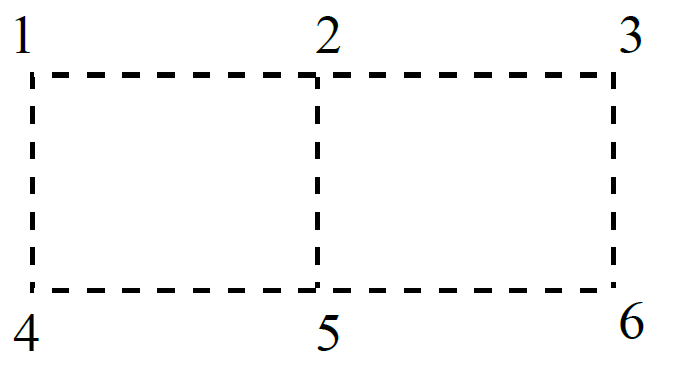
工程師發現只要用 $5$ 段光纖就可以將這 $6$ 個設備連接起來，下圖為兩種可能的連結方法，事實上還有其他連結的方式。工程師想知道總共會有幾種相異的連結方法，可以用最少的線段把所有的網路設備連結起來。

一般而言可將上述平面架構圖延伸為 $2N (N \geq 3)$ 個頂點，上排頂點的編號為 $1$ 到 $N$，下一排的頂點編號由 $N+1$ 至 $2N$，其中頂點 $I (1 \leq I \leq N)$ 與頂點 $I+N$ 相鄰，另外對於頂點 $I (1 < I < N， N+1 < I < 2N)$ 分別與頂點 $I-1$ 及 $I+1$ 相鄰。請寫一程式，幫工程師計算出總共有幾種相異的連結方法。因答案可能很大，程式輸出的答案為「原始答案」除以 $10^ 9+9$ 的餘數。

條件限制

• 有 $T$ 筆輸入，$T \leq 10$
• $1\leq N \leq 100$