給 $n$ 個整數,求每個數往左邊看、第一個比它小的數字的編號,沒有這種數字的話輸出 $0$。
條件限制
- $1 \leq n \leq 2 \times 10^5$
我們先把題目說得視覺化一點:有 $n$ 個人站成一排,第 $i$ 個人的身高是 $x_i$,每個人都會往左看,找到最近的比他矮的人。
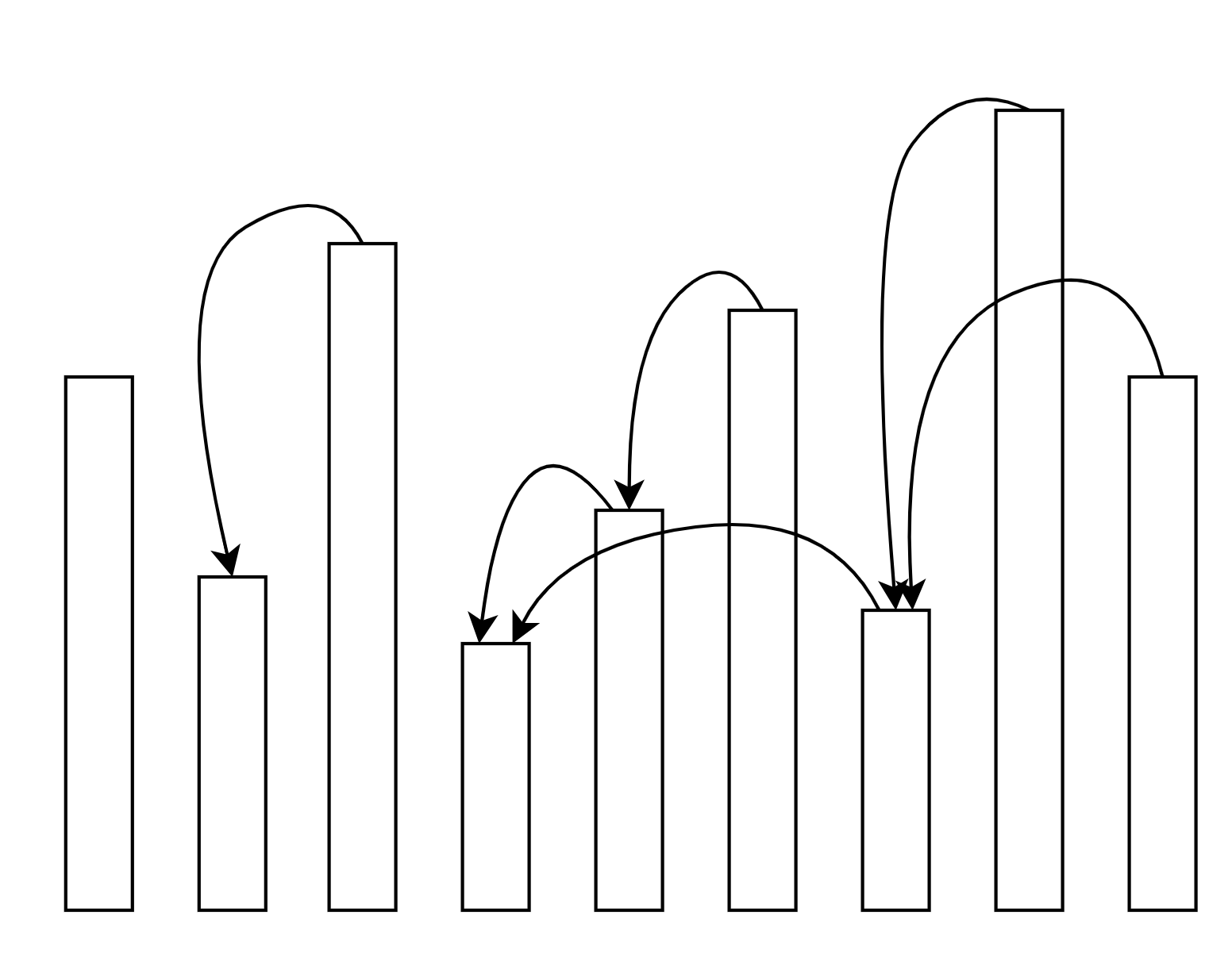
要直接通靈出一個人的答案,好像有點困難,這種時候就可以秉持掃描線精神,從左邊開始枚舉,並且用我們以前看過的資訊來找到現在看到的人的答案(畢竟答案就在左邊嘛)。我們試著從左邊第一個人開始,依序決定每個人的答案。要是某個人是第 $i$ 個人的答案,他理所當然就只能比第 $i$ 個人矮,所以如果我們讓左邊身高 $\geq x_i$ 的人都直接「退出隊伍」,那留下來的人之中,站最右邊的就是 $i$ 的答案了。可以想像成整個過程是,我們從第 $1$ 個人開始,依序呼叫每一個人,當第 $i$ 個人被叫到的時候,他就會叫所有在他左邊、身高 $\geq$ 他的人都離開隊伍,然後他就會知道他的答案是站在他左邊的第一個人。
先不論要怎麼有效率的維護還在隊伍裡面的人,我們先確認一下這個作法是不是正確的。要是我們直接讓那些長太高的人永遠離開隊伍,可能會有一個問題:會不會他們有可能是更右邊的人的答案?其實不會,要是有個人 $j$ 被第 $i$ 個人趕出隊伍了,我們就知道 $j < i$、$a_j \geq a_i$,對於一個位置比 $i$ 還右邊的人 $k$,他的答案絕對不會是 $j$,這是因為如果他的答案是 $j$,那就有 $a_j < a_k$,根據我們剛才知道的資訊,$j < i < k$、$a_i \leq a_j < a_k$,$i$ 也是一個比 $k$ 矮的人,而且還離 $k$ 更近,所以答案當然就不會是 $j$。舉例來說,上面那張圖裡面,左邊數過來第二個人比最左邊的人矮,那所有右邊的人往左看比較矮的人的時候,當然是會先看到第二個人。
換個角度講,對於一個人 $j$ 來說,一旦他右邊有一個身高一樣,或是比他更矮的人 $i$,那 $j$ 就不會是比 $i$ 更右邊的人的答案,也就是說,當有一個身高 $\leq x_j$ 的人,在 $j$ 之後被叫到了,那 $j$ 這個人就永遠沒有用了,他就可以放心地直接離開隊伍。
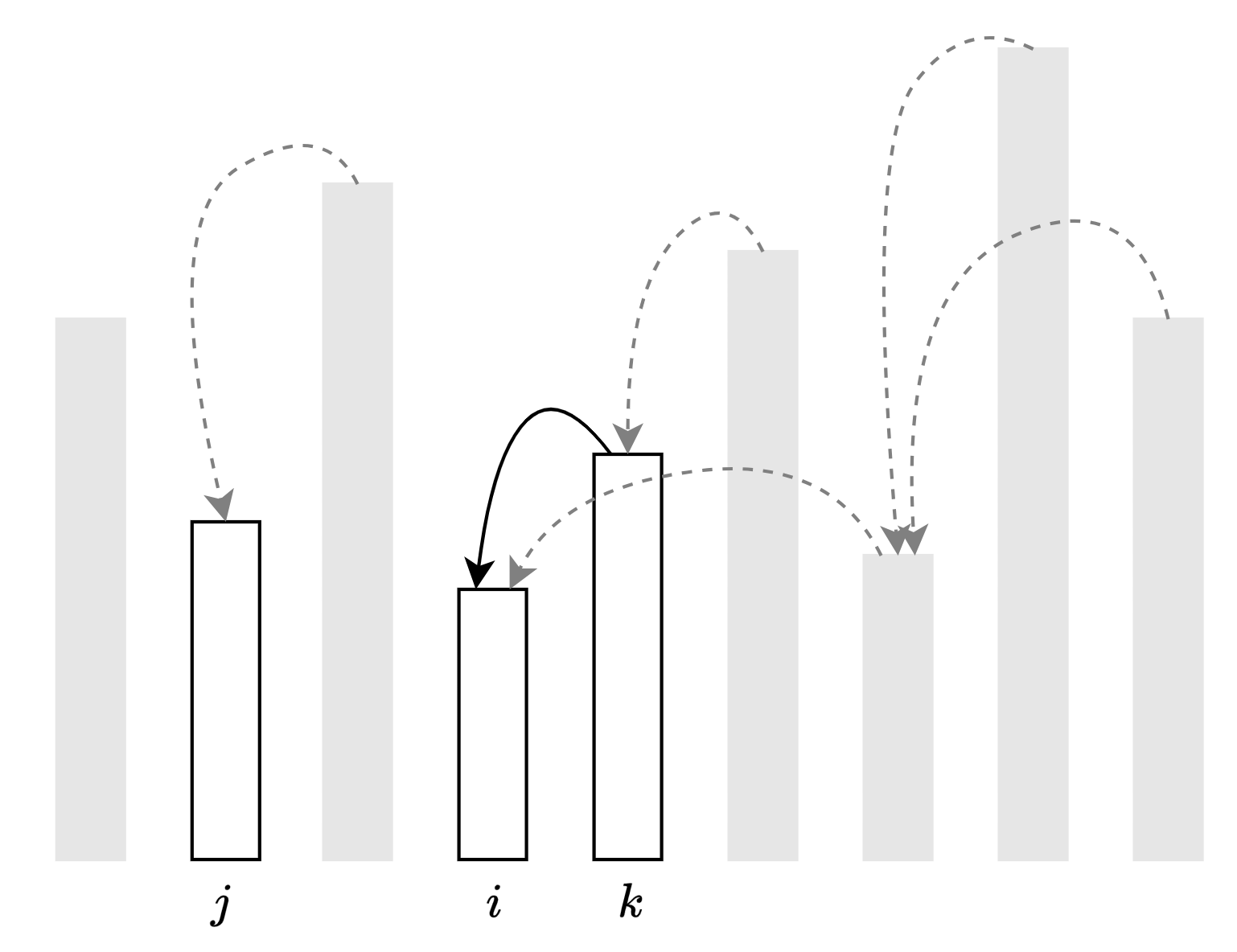
像是在上圖裡面的 $j$,在我們叫到 $i$ 的時候,我們就知道 $j$ 既不會是 $i$ 的答案,也不會是之後的人(例如 $k$,即便 $k$ 比 $j$ 還高,但中間夾了一個更矮的 $i$)的答案,因此 $j$ 在此時就可以退出隊伍了。
那我們要怎麼知道現在誰要被踢出隊伍、留在隊伍裡面,$i$ 之前的最右邊的人是誰呢?先來看看留在隊伍裡面的人會長什麼樣子:
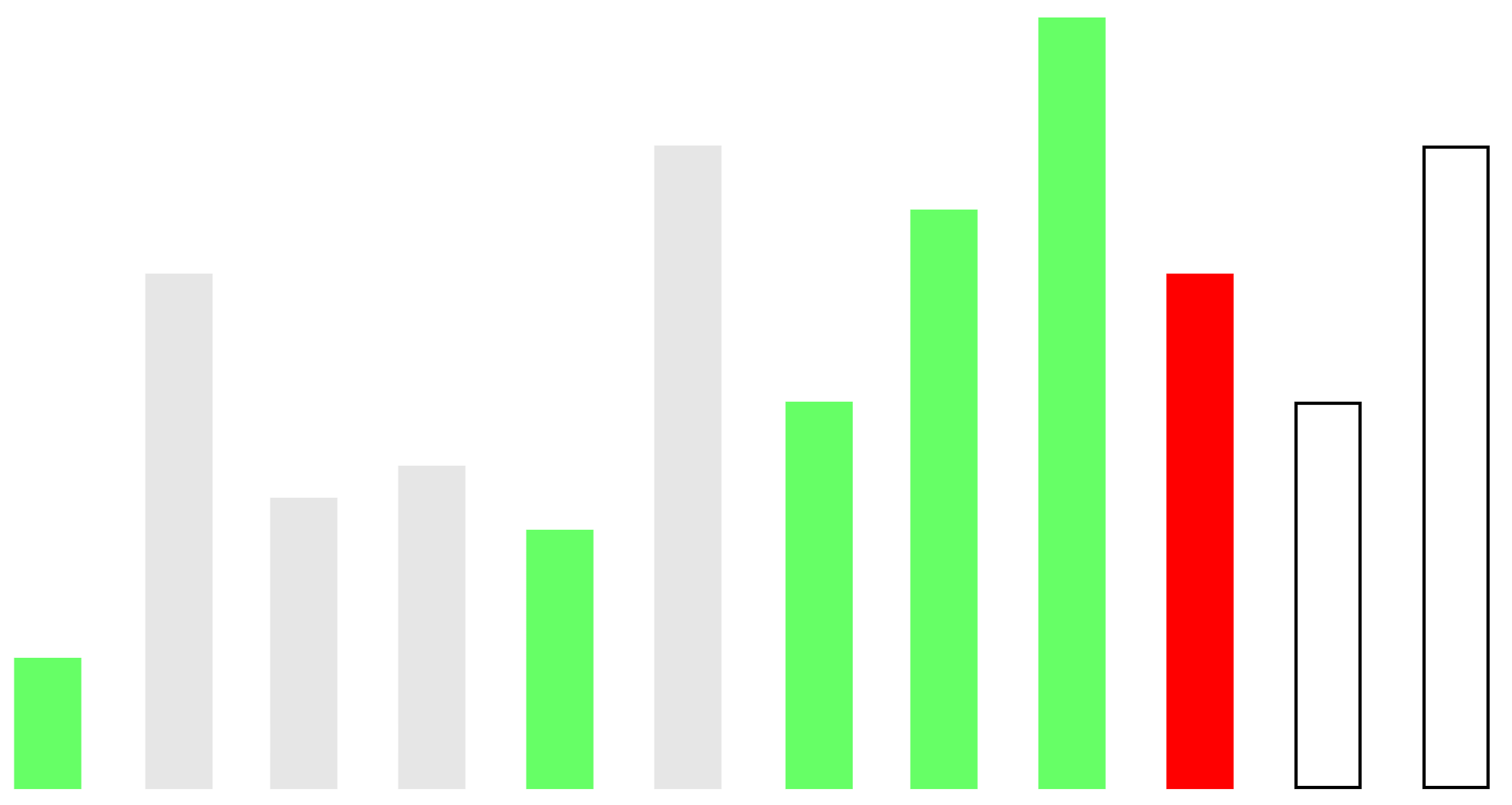
紅色是我們現在叫到的人,綠色是左邊還留在隊伍裡的人,右邊的人還沒被叫到所以先不理他們。注意到已經被叫過、留在隊伍裡的條件是「右邊沒有一樣高或更矮的人被叫到過」,所以那些被叫到之後還留在隊伍裡的人(綠色那些人),由左至右會是嚴格遞增的,當我們要讓身高 $\geq$ 紅色的人離開隊伍時,這些人一定是最靠右的那些綠色的人。
講得更明白一些,可以想像成是我們讓被叫過的人去待在一個額外的隊伍裡面,當我們叫到一個人 $i$ 時,就讓額外隊伍裡,身高 $\geq$ 他的人都離開隊伍,額外隊伍裡的最後一個人,就是 $i$ 的答案,然後讓 $i$ 去排在額外隊伍的最後面。這個額外隊伍永遠都會保持嚴格遞增,所以那些要退出隊伍的人,總會是隊伍的最後幾個人,我們只要不斷檢查最後一個人,他太高了就叫他離開,直到最後一個人比 $i$ 還矮或額外隊伍空了為止。也就是說,這個額外隊伍就是一個 stack!我們用一個 stack 維護這個額外隊伍,就可以解決這個問題了。
#include <bits/stdc++.h>
using namespace std;
int main () {
int n;
cin >> n;
stack<int> stk;
vector<int> x(n + 1);
for (int i = 1; i <= n; i++) {
cin >> x[i];
while (!stk.empty() && x[stk.top()] >= x[i])
stk.pop();
if (stk.empty()) cout << 0;
else cout << stk.top();
cout << " \n"[i == n];
stk.push(i);
}
}
喔不,這個程式碼裡有兩層迴圈!用不著擔心會 TLE,每次 while 迴圈成功執行的時候,都會丟掉一個 stk 裡的東西,而每個人都只會被放進 stk 一次、最多有 $n$ 個東西被放進 stk,因此裡面的 while 迴圈最多只會被執行 $n$ 次,總時間複雜度是 $O(n)$。(還記得我們在基礎演算法 / 複雜度提過的「一個沒那麼單純的例子」嗎?)
剛才我們維護的額外隊伍,因為保持單調遞增的特性,就被稱為單調隊列(monotonic queue,也有人會叫它單調 stack,但這個我們等等再說)。單調隊列不一定是要維護嚴格遞增,也可以是遞減或是非嚴格,就只要改一下上方程式碼第 11 行 pop 條件中的 >= 就好。
| 候選答案的單調性 | pop 條件 |
|---|---|
| 嚴格遞增($<$) | $\geq$ |
| 嚴格遞減($>$) | $\leq$ |
| 非嚴格遞增($\leq$) | $>$ |
| 非嚴格遞減($\geq$) | $<$ |
單調隊列在維護的東西其實就是「候選答案」,當一個元素將來再也不會是答案,我們就可以把他丟掉,而單調隊列就是利用「每次會變得沒用的人非常好找,很好維護」的特性,有效率的達到目標。
就像這張表一樣,在使出單調隊列的時候,有兩種方向可以想:一個是像剛剛一樣,思考一個元素沒有用的條件是什麼,另一個就是想想看剩下來的有用東西會有什麼關係,這兩個條件是相反的(像是要維持 $x_i < x_j$ 就是要避免 $x_i \geq x_j$ 出現)。大部分人在描述如何用單調隊列解一道特定題目的時候,都會直接說「維護一個嚴格遞增的單調隊列」之類的話,不過有時候要直接想出要維護的性質為何會比較不直覺,發現一個方向不好想時不妨從另一個方向下手。
給你一個長度為 $n$ 的陣列 $a_1,a_2,\dots,a_n$ 和一個數字 $k$,求所有長度為 $k$ 的區間中的最大值與最小值。
條件限制
- $n \leq 10^6$
- 要開 long long
- $k$ 可能會大於 $n$
我們先找最小值看看。用和剛剛一樣的想法,我們由左至右逐一決定每個長度為 $k$ 的區間的最小值,假設我們現在在看以第 $i$ 個元素為最右邊元素的區間,也就是要找 $a_{i-k+1},a_{i-k+2},\dots,a_i$ 的最小值。既然要用單調隊列,我們就先來想每個元素會變得沒用的條件:
- 所有 $j < i-k+1$ 的 $a_j$ 再也不會出現在我們要求答案的區間裡了,所以它將來都沒有用。
- 既然我們要求的是「區間最小值」,那要是有一個元素 $a_j$ 右邊有個 $a_k$ 更小,那它對於以 $i \geq k$ 為右界的區間都絕對不是答案。
第二個條件簡短地說就是「一個元素遇到右邊有人更小就會沒用」,所以我們可以在看到以 $i$ 為右界的區間時,讓左邊所有比 $a_i$ 還大的元素離開隊伍,這樣一來目前隊伍中有用的元素就會是非嚴格遞增,區間 $a_{i-k+1},a_{i-k+2},\dots,a_i$ 的答案就是隊伍之中,位置在 $i-k+1$ 以後的第一個元素。第一個條件跟我們說,$i-k+1$ 之前的元素其實已經沒有用了,所以我們可以放心地也讓它們視為離開隊伍,這樣一來隊伍中第一個元素就是答案了。
現在,我們要用來維護隊伍的資料結構其實不再是一個 stack 了,因為我們多了「讓在隊伍前面的人離開隊伍」的操作,所以我們要換成用一個 deque。
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
int n, K;
while (cin >> n >> K) {
if (K > n) K = n;
vector<ll> a(n + 1);
for (int i = 1; i <= n; i++) cin >> a[i];
vector<ll> ans_min(n + 1), ans_max(n + 1);
deque<int> dq; // 在隊伍裡面的元素編號
for (int i = 1; i <= n; i++) {
// 右邊有更小數字的元素就沒用了
while (!dq.empty() && a[dq.back()] > a[i])
dq.pop_back();
// 太左邊的元素就沒用了
if (!dq.empty() && dq.front() < i - K + 1)
dq.pop_front();
dq.push_back(i); // 把 i 放進隊伍
ans_min[i] = a[dq.front()]; // 答案是隊伍裡最左邊的人
}
// 自己寫找最大值的版本!
for (int i = K; i <= n; i++) cout << ans_min[i] << " \n"[i == n];
for (int i = K; i <= n; i++) cout << ans_max[i] << " \n"[i == n];
}
}
其實就是我們前面在做的單調隊列,只不過存在於隊伍裡的元素僅限於我們考慮的區間之中。像這樣維護一個不斷移動的固定長度區間的作法,被稱為 sliding window。
單調隊列的經典應用就是剛才看到的那兩種:
- 找出一個序列中,每個數字左 / 右第一個比較大 / 小的數。
- 找出一個序列中,所有長度為 $k$ 的區間中的最大 / 小值。
在需要做這兩種事情的時候,直接用單調隊列就對了。接下來我們再講一些稍微變形的例題來幫助讀者熟悉一下怎麼使用單調隊列。
給一個 $1 \sim n$ 的排列 $p_1,p_2,\dots,p_n$,求它的笛卡爾樹(Cartesian tree)。笛卡爾樹的定義是:
- 令 $p_r$ 為序列中的最小值,節點 $r$ 是整棟樹的根。
- $r$ 的左子樹是 $p_1,\dots,p_{r-1}$ 的笛卡爾樹,右子樹是 $p_{r+1},\dots,p_n$ 的笛卡爾樹。空序列的笛卡爾樹就是空的。
條件限制
- $n \leq 10^7$
舉例來說,$[2, 8, 3, 1, 9, 5, 7, 4, 6]$ 的笛卡爾樹長這樣:
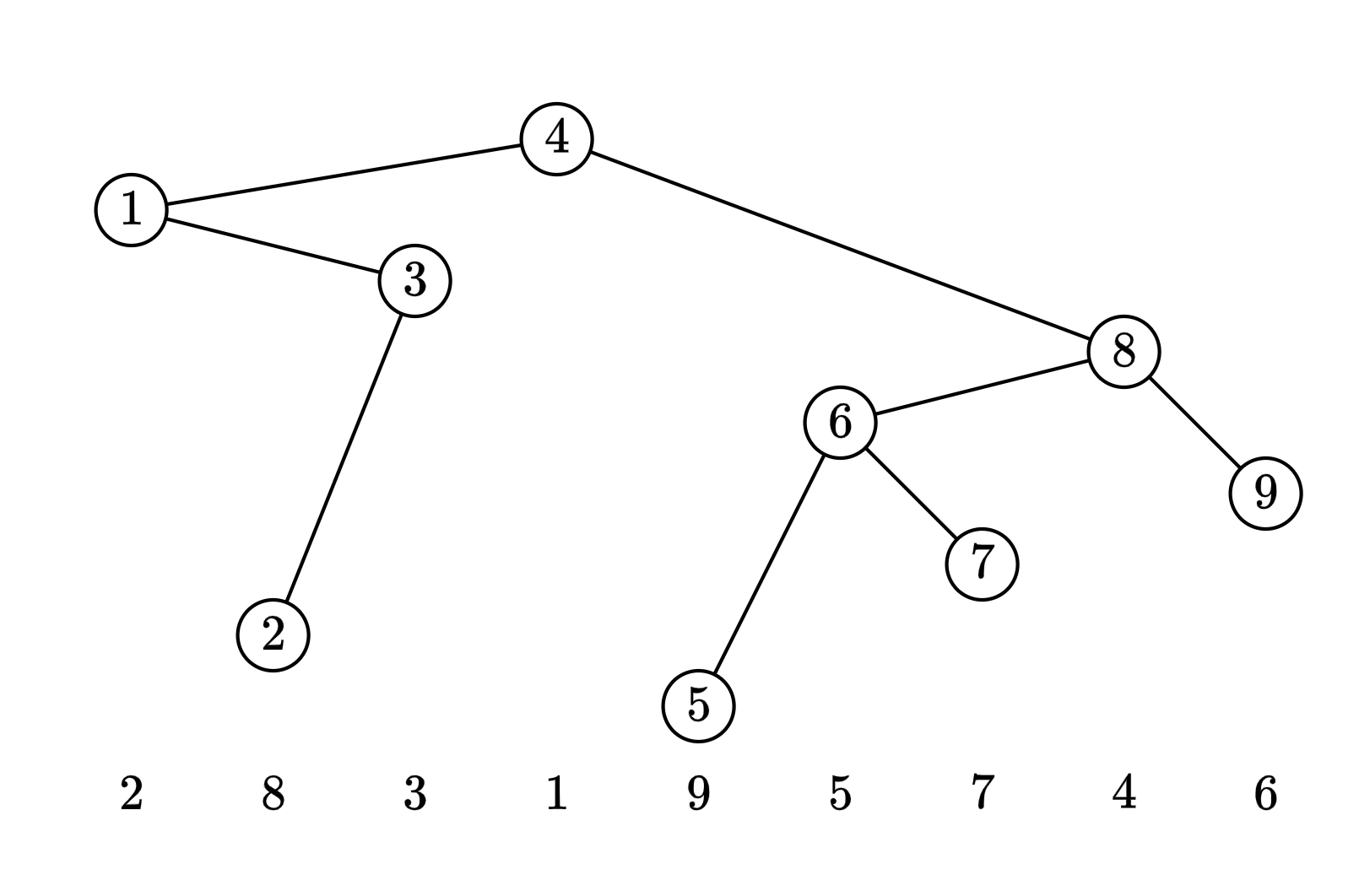
笛卡爾樹的性質我們就先不詳細探究,直接說我們要用的結論:仔細看一下上面這張圖就會發現,一個節點的父節點,就是「左右第一個數值比較小的人之中,比較大的那一個」,所以只要先找每個數左右第一個比它小的人,再看哪個比較大,就知道它的父節點是誰,而這剛好就是能用單調隊列直接解決的問題。
不過,左右第一個比較小的都要找,要正反跑一次也太累了吧?其實我們只要跑一次單調隊列就能找到左邊跟右邊的答案了。如果我們只要找左邊第一個比較小的話,從左看到右邊,一個數會變得沒有用的時機是「我們看到一個比它更小的數」的時候,所以一個人被從隊伍(我們維護的那個 stack)中踢掉時,就代表我們現在看到的數,就是它右邊第一個比它小的數!統整一下,完整的流程是:
- 有一個額外的隊伍(實際上是一個 stack),一開始的空的。
- 枚舉 $i=1,2,\dots,n$:
- 看隊伍裡的最後一個數 $p_j$,如果 $p_j > p_i$ ,$p_j$ 以後都沒有用了,把它丟掉,此時我們得知 $p_i$ 是 $p_j$ 右邊第一個比較小的數。重複直到隊伍裡空了或 $p_j < p_i$ 為止。
- 如果隊伍裡面有東西,最後一個是 $p_j$,那麼我們得知 $p_i$ 左邊第一個比較小的數是 $p_j$。
這樣就可以同時找到左邊和右邊第一個比較小的數了。有一件事情要特別注意,因為這題的輸入是一個排列,每個數字都不一樣,所以我們還不需要擔心相等數字的問題,但如果有相等數字的時候會發生什麼事?
先換個符號以免搞混,我們要對一個數字可能有重複的序列 $a_1,a_2,\dots,a_n$ 找每個數左右第一個嚴格小的數,然後按照一樣的路線走:當我們看到 $a_i$ 的時候,我們希望在把隊伍裡面沒用的人踢掉之後,最後一個人就是 $a_i$ 左邊的答案,因此 $a_j$ 變得沒用的條件就是 $a_j \geq a_i$,等於的人必須被踢掉,如此一來可以找到每個人左邊第一個嚴格小的數沒錯,但一個數被踢出隊伍的時機會變成「遇到第一個小於等於它的人的時候」,要是直接把它被 pop 的時機當作答案那就錯了,此時還是左右分開做比較方便。
上網查笛卡爾樹的話可能會查到一個「用 stack 維護最右側鏈」的作法,那其實也是用單調隊列,只是在維護單調隊列的過程改用「找出每個節點左右子節點」而非找父節點的角度去看,想起來會稍微複雜一些,但寫出來會比較精簡,有興趣的讀者可以自行搜尋。
有 $N$ 棟房子排成一列,其中由左至右第 $i$ 棟房子的高度是 $H_i$。對於兩棟不同房子 A、B 來說,如果房子 A 與房子 B 之間的所有其他房子,高度都 $\leq$ A 和 B 的高度,則站在房子 A 上的人可以看到房子 B。
令第 $k$ 棟房子上的人能看見的其他房子數量為 $C_k$,求 $C_1+C_2+\dots+C_N$。
條件限制
- $N \leq 10^6$
- $H_i \leq 10^9$
「可以看到」的關係是雙向的,A 能看到 B 那 B 就能看到 A,所以我們只要數「每棟房子往左看會看到幾棟房子」,加起來再乘 2 就是答案了。同樣地,我們從最左邊的房子開始,一一找每一棟房子往左能看到幾棟房子,這次我們改用「看得見的房子會有什麼性質」來想,很直覺地就會想到,一棟房子往左看時,能看見的房子由左至右要非嚴格遞減,所以反過來說,沒用的時機就是出現一棟更高的房子,那較矮的房子就會被擋住,因此 pop 條件是左 $<$ 右。
至於答案要怎麼算呢?在看到房子 $i$ 的時候,只有先前剩下來的有用房子才可能被它看見,而那些被它 pop 掉的房子,根據非嚴格遞減的性質,它們和 $i$ 之間都不會有更高的房子,因此 $i$ 肯定都看得見它們。要是 pop 完之後還有有用的房子,那最右邊那一棟有用的房子也是看得見的,這個時候數量要 $+1$……只寫這樣就會獲得 WA,舉例來說,$N=3$,三棟房子的高度分別是 $3,2,2$,在看到第 3 棟房子的時候,因為前兩棟房子都還是有用的,那就只會數到 1 棟可以看見的房子,但兩棟房子都是看得見的!
問題點在於,實際上能看到的房子除了那些剛剛 pop 掉的以外,還有剩下來的有用房子中,最後那些跟現在看到的房子一樣高的,還有再前一棟房子也看得到。然而,暴力檢查有幾個一樣高的房子的話,有可能每看到一個新房子時,都得花 $O(N)$ 的時間做這件事,總時間就會噴到 $O(N^2)$ 了。一一檢查行不通,不如我們把有用房子之中,連續的那些一樣高的合併起來,反正它們要變成沒用就是全部一起變成沒用。我們用一個 pair $(\text{房子的高度},\text{數量})$ 來表示 stack 中維護的有用房子。
#include <bits/stdc++.h>
using namespace std;
using pii = pair<int, int>;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
int n;
cin >> n;
stack<pii> stk; // (高度, 數量)
long long cnt = 0;
for (int i = 0; i < n; i++) {
int h;
cin >> h;
// 比較矮的房子以後都沒用了,直接 pop 掉
while (!stk.empty() && stk.top().first < h) {
cnt += stk.top().second; // 全部都看得到
stk.pop();
}
// 如果最後一段房子跟這棟一樣高
if (!stk.empty() && stk.top().first == h) {
cnt += stk.top().second; // 全部都看得到
stk.top().second++; // 直接把數量 +1
}
else stk.push(pii(h, 1)); // 最後一段不一樣高的話要自己開一段
// size >= 2 代表除了最後一樣的那一段之外還有東西,再前面一個是看得到的
if ((int) stk.size() >= 2) cnt++;
}
cout << cnt * 2 << "\n";
}
這樣一來就也在 $O(N)$ 的時間做完了。
介紹了這麼多例題,相信讀者已經很熟悉使用單調隊列的固定模式了:找出讓東西變得沒用的條件,或是「似乎」有用的東西之間的關係、維護「似乎」有用的東西、再從剩下有用的東西中找到答案,而維護的「有用性質」(也就是單調性)會讓丟掉沒用東西和從有用東西找出答案特別方便,從而給出好的複雜度。就如上面所有例題一樣,單調隊列的題目往往都有包裝,需要自己發現可以使用單調隊列。左右第一個較大 / 小值和 sliding window 極值就是最經典的兩類可以被單調隊列做掉的問題,要用單調隊列的題目大多時候都可以轉換成這兩種問題。單調隊列也有其他種變形,核心精神都是「有用的東西很好維護」,讀者未來學到一些進階的技巧時就會遇到了。
最後,我們回來提一下「單調隊列」這個稱呼,剛才我們用來實作單調隊列的資料結構是 stack 或 deque,都不是名稱中的隊列(queue),有些人會把只使用 stack 操作(只需要從一端插入刪除)的單調隊列叫作單調 stack,不過裡面使用的資料結構是什麼其實沒有很重要,根據要做的操作使用對應的資料結構就好。
別忘了在 C++ 中,stack 和 queue 預設都是用 deque 實作的,只需要 stack 操作的時候,可以改用 vector 來減少常數。
有 $n$ 個大樓排成一列,從左到右第 $i$ 棟的高度是 $a_i$,寬度都是 1,這些大樓都緊緊相鄰,你要在這些大樓上貼一個長方形廣告看板,使得整個看板背後都貼在這些大樓上,且底邊和地面平行。求這個看板的面積最大可以是多少。
條件限制
- $1 \leq n \leq 2 \times 10^5$
- $1 \leq a_i \leq 10^9$
有一個 $M \times N$ 的 01 表格,求最大的全部都是 1 的矩形大小。
條件限制
- $M,N \leq 200$
有 $N$ 個資料庫 $1,2,\dots,N$,每個資料庫有各自的通訊半徑 $r_i$ 和保密等級 $s_i$,兩個資料庫 $i,j$ 可以直接通訊的條件是(假設 $s_i < s_j$)
- $\lvert i - j \rvert \leq \min(r_i,r_j)$,且
- 對於所有 $k$ 滿足 $\min(i,j) < k < \max(i,j)$,滿足以下所有條件:
- $s_k < s_j$。
- $s_k < s_i$ 或資料庫 $k$ 不能和 $i$ 直接通訊。
不能直接通訊的資料庫可以透過其他資料庫傳訊息,令 $f(i,j)$ 是 $i$ 要傳訊息給 $j$ 最少需要經過幾次直接通訊,給定 $S$,求 $\sum_{i=1}^N f(S,i)$。
條件限制
- $2 \leq N \leq 10^6$
- $\forall i \neq j,\ s_i \neq s_j$