你即將舉辦一場派對,為了迎接客人,你決定拿出你的拿手好菜──煎餅!為了準備,你拿出了一個很特殊的鐵盤,在這個鐵盤上做的所有的煎餅都會是排成一直線的。
就在你煎得很快樂時,你的常用鍋鏟突然不見了,眼見還有很多煎餅需要翻面(不然會焦掉),你迅速找到了一把造型奇特的鍋鏟,它的長度是 $k$,代表它只能一次為恰好連續的 $k$ 個煎餅翻面!
焦急的你面臨這樣的問題,假設我們簡化煎餅的配置成一個字串 $s$,代表哪些煎餅是需要翻面的、哪些是已經翻過面的,你可以迅速找到「使得所有煎餅都翻面」所需的最小次數嗎?
條件限制
- $T\leq 10^6$ 筆測資。
- $1\leq k\leq 10^6$
- 所有測資中的字串 $s$ 總和 $\leq 10^6$。
這題有一個很單純的策略:每次找到最左邊需要翻面的煎餅,並將鍋鏟的最左側貼在他身上後翻面。
- 這是因為對於最左邊那個煎餅,也只有一種翻法可以翻到他,在處理好最左邊的煎餅後,就可以把最左邊的煎餅遮住當作沒看到。
不過此時有個新手會不小心忽略的問題:假設 $n$ 是字串的長度,整個鐵盤可能會需要翻到 $O(n-k)$ 次,如果 $k=\frac{n}{2}$,每次翻面又需要花 $O(k)$ 的時間,會直接讓時間複雜度大至 $\Theta(n^2)$!
以往要加速貪心的過程,似乎只需要排個序就完成了,但這在這題似乎行不通。
不妨仔細想像我們執行策略的過程,假設我們就正常的從左邊一路翻過來好了,當我們看到第 $i$ 個煎餅時,其實我們會在乎的是
- 他左邊的 $k-1$ 種操作被執行的總次數。
也就是說,對於他左邊的 $k-1$ 種位置,如果我們有試圖用鍋鏟將其貼在最左邊翻一次的話,這個煎餅就會跟著被翻一次,而這個次數的奇偶性、和這個煎餅的初始狀態其實就決定了當前這個煎餅的狀態!
另一方面來說,對於一次翻面操作,可以想像他就是一口氣讓連續的 $k$ 個煎餅身上被翻動的次數 $+1$,此時我們可能會需要能快速支援
- 對一個區間加上 $1$。
看到這樣的操作有想起什麼嗎?沒錯,就是我們在基礎演算法 / 前綴和與差分學過的差分!
如果仔細想一遍當初講解過的區間加值問題,就會發現因為我們的加值操作剛好是從左到右的,所以我們其實可以邊加、邊把最後的序列還原,這也就能同時幫助我們在 $O(1)$ 時間加值、$O(1)$ 時間得到當前煎餅的狀態。
因此,透過結合我們先前學過的知識,我們便成功加速了這個貪心策略到 $O(n)$ 時間。
給你 $N$ 個數字 $a_1, a_2, \cdots, a_N$,請把這些數字加起來。很簡單?但是但是,要加兩個數字 $x$ 和 $y$ 有一個條件:必須付出 $x + y$ 的代價。請問要把這 $N$ 個數字加起來的最小代價為何?
例:如果 $N = 3$ 且數列為 $[1, 2, 3]$,則最好的作法就是先加 $1$ 和 $2$,花 $3$,再把兩個 $3$ 加起來,花費 $6$,總共花費 $3 + 6 = 9$。
條件限制
- $1\leq N\leq 10^5$
- 所有數字均為正整數,且小於 $10^8$。
讀者可以稍微模擬一些狀況,找找看最佳的「加法」順序到底是多少。
一個最直覺的想法便是找出最小的兩個數字將他們相加,而加完之後由於他們會形成新的數字,就當成規模少一的問題不斷做下去就行了。
也就是說,我們的貪心策略便是:不斷找出最小的兩個數字相加,直到剩下一個數字為止。
這個策略為什麼是正確的呢?他的證明其實有些複雜,直覺上可以想成是在計算加法的過程中,會希望盡量大的數字被加盡量少次,所以先處理較小的數字總是比較好。如果想看更嚴謹的證明的話,可以自行展開以下證明。
我們可以將加法的過程想成蓋出一棵二元樹的過程,滿足每個數字對應到二元樹的一個葉節點,每個加法會製造出一個新的二元樹節點,數值是剛得到的總和、而左右小孩分別就是拿來加法的兩個數字所代表的節點。
可以發現,如此一來就可以把總花費想成是所有數字乘上「他所在的深度」總和,也因此,令最小的兩個數字為 $a$ 和 $b$,對於最佳合併的方法我們會有
- 將 $a$ 和 $b$ 與最深的一對執行加法的兩個節點互換後,答案不會變差。
所以我們得出結論:在最佳策略中,總是會把最小的兩個數字相加。因此要解整個問題時,先執行這一步並不會造成問題,此時得到一個規模少一的子問題後,根據數學歸納法可以得證整個演算法的正確性。
既然我們相信我們的貪心策略是正確的,那就是該來優化其時間複雜度的時間了。很明顯的,因為每次都要找到最小的兩個數字,加法又需要執行 $N-1$ 次,所以需要的總時間會是 $O(N^2)$ 的,肯定會超時。
不過,如果我們好好的把這個過程想成一個資料結構問題,會發現其實我們需要支援的是以下操作:
- 支援從資料結構中拿出最小值。
- 支援加入一個新的數字進入資料結構。
沒錯,我們的每一次加法其實就是「拿最小值」、「拿最小值」、「加入數字」三個上述資料結構的操作。而看著上述的敘述,想必讀者應該也發現了,這正是我們的 priority queue 能在 $O(\log N)$ 時間內辦到的!
綜上所述,我們便能在 $O(N\log N)$ 的時間內通過這題。如果讀者忘記 priority queue 怎麼使用,可以到基礎資料結構 / Heap 複習。
現在軌道上有一輛火車由 $n$ 節車廂構成。車廂的編號由前往後分別是 $1,2,3\cdots n$。在很久以前,有建置三角線來調度與排列車廂。但由於財政拮据,這些線路都被變賣拆除了,你只能使用現有的車站軌道來排列車廂。
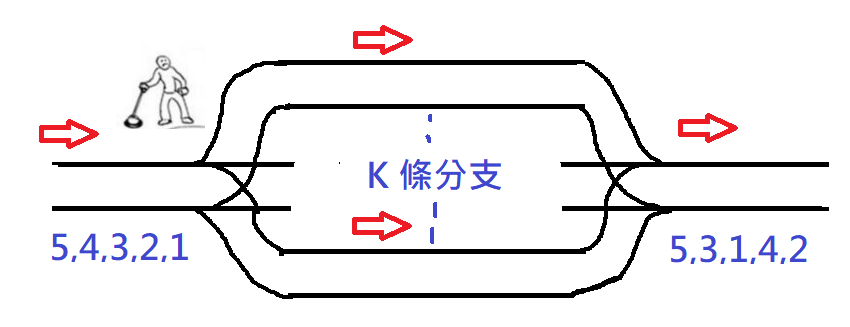
車站有 $k$ 條軌道可以使用,我們假定任意一條軌道都有能力存放所有車廂。每次可以將列車最前面的一節車廂推入車站內任意一條軌道中;或是將在車站軌道內的車廂推出車站,過程中車廂不能倒退行駛。
以上圖為例,如果想將有 $5$ 節車廂的列車編號重新排列成 $2,4,1,3,5$,而車站只有兩條軌道可以使用的話,可以先將 $1$ 車廂推入上方軌道;$2$ 號車廂由下方軌道堆入後,再推出車站;再將 $3$ 車廂推入上方軌道;$4$ 號車廂由下方軌道堆入後,再推出車站。然後將上方軌道的 $1,3$ 車廂推出車站。最後的 $5$ 號車廂使用任意軌道推出即可完成要求。
然而在不斷推送車廂的過程中,發現了似乎有某些排列是無法完成的,給定車廂的數量以及車站軌道分支數,你可以判定要排列的車廂順序是否可以被完成嗎?
條件限制
- $1 \leq n,k \leq 10^5$
注意到我們可以先把數字重新換個順序,讓目標的排列恰好是 $1\sim n$。因此接下來我們就不失一般性的假設目標排列是 $1\sim n$。
這題乍看之下真的不太好思考,如果想要找出貪心選擇,難道是每次要選擇一個最好的數字丟進最好的軌道嗎?
別忘了我們從貪心法 II 學過的,面對這種題目,我們會需要先看出題目的本質才會比較好思考。
注意到單一軌道內的數字在進入後就無法改變相對順序了,當所有數字都進入軌道後,我們所能控制的,就只有他們從軌道出來的順序。因此,其實問題可以重新改寫成以下形式:
- 給定一個排列,請問他是否能拆成 $k$ 個子序列,滿足每個子序列都遞增?
更直接一點,我們可以直接來解這個問題:
- 給定一個排列,請問他是能拆成最少幾個子序列,滿足每個子序列都遞增?
從這個角度思考,我們似乎可以一個一個數字從左到右照順序看過去,維護盡量少個子序列,滿足每個都遞增;在遇到一個新的數字後,找到一個最好的子序列把它放在後面就好,如果沒有符合的子序列,才新增一個。
這樣的策略只剩下最後一個疑慮:
- 在遇到一個新的數字後,哪一個子序列才是對他來說最好的呢?
很明顯的,該數字如果是 $x$,那他能放在後面的子序列尾端的數字肯定得 $<x$,若沒有這樣的子序列,$x$ 就得新開一個子序列。
當有多個子序列可以讓 $x$ 做選擇時,其實有一個很乾脆的結論:
- 選擇這些可選子序列中,尾端最大的那個。
證明其實也很單純,假設這個最大的尾端是 $b$,最佳解卻選擇了 $a$ 的話,我們與最佳解在這瞬間的差異就是兩個子序列的尾端:最佳解是 $\{b, x\}$、我們則是 $\{a, x\}$。可以發現,我們「後續能承受的」只會比這個所謂的最佳解還要更寬裕,也就間接證明了最佳解可以直接貼合我們的策略。
不過事情當然沒那麼單純,一樣的,因為我們每次放數字都可能有 $k$ 個子序列要考慮,這會讓時間複雜度直接上升到 $O(nk)$,實在不太樂見。
我們不妨先假設這 $k$ 個子序列已經按照尾端排好了,觀察看看新的數字加進來後會發生什麼事:
如果原本的序列如下所示,要加進來的數字是 $6$,則他會放在下列紅色的數字所代表的子序列後方:
$$
1\ 3\ \color{red}{5}\ 8\ 9
$$
放完後會變成
$$
1\ 3\ \color{red}{6}\ 8\ 9
$$
讀者是否有發現什麼呢?放完之後,整個序列還是遞增的!而且這個性質就算是遇到「新增一個子序列」的情況,放在最後面也當然是吻合的。
這代表說,我們每次其實就只是嘗試在一個遞增的序列中,找到 $< x$ 中的最大位置,好好與我們學過的技巧做連結——這個不正是一個二分搜能辦到的事情嗎?
因此,利用二分搜來模擬數字放在後方的過程,整體就是一個 $O(N\log N)$ 的演算法。
有一條數線上有 $N$ 個服務點,第 $i$ 個服務點的座標在 $P[i]$,並且你可以選擇最多 $K$ 個位置(可以在任意位置,也不一定要整數座標)設置基地台。你的目標是決定一個基地台的服務半徑 $R$,滿足有辦法設置基地台,使得每個服務點距離 $\leq R$ 以內都至少有一個基地台。求最小的 $R$。
條件限制
- $1 \leq K < N \leq 50000$
- $0 \leq P[i] \leq 10^9$
讓我們回顧一下放在基礎演算法 / 對答案二分搜的這道習題。按照當時所學的,這題很直接就是先對答案二分搜,將問題轉化成「當服務半徑是 $R$ 時,最少要蓋幾個基地台才能蓋住所有服務點」。
注意到此時,我們可以把一個基地台的設置想成是我們把一個長度為 $2R$ 的區間覆蓋在數線上,而最後要的就是讓所有服務點都被區間蓋住。相信讀者都來到這裡了,便能直接想出最為單純的貪心策略:每次找到最左邊還沒被覆蓋的那個服務點後,直接設置一個基地台使得他的區間左界蓋著這個服務點。
這樣的問題能給我們什麼啟發呢?有些讀者可能沒有意識到,但實際上包含我們在基礎演算法 / 對答案二分搜所學的,這些問題很多都是先對答案二分搜後,變成在解一個「貪心法」的問題!
換句話說,一道貪心法的題目並不一定會裸裸的呈現在我們面前的,反而很有可能需要經過一層拆解才能可以得到我們要需要解的問題——在這裡,我們就是透過對答案二分搜來拆解出背後的貪心法題目。
在這個章節,我們了解到了兩種貪心可能可以跟其他領域結合的可能性:
- 先得出一個貪心策略,再使用資料結構優化。
- 貪心法的題目可能會藏在一層包裝下——在本文章中,我們了解到先「對答案二分搜」會是一種常見的包裝。
當然,看過這些例子後,相信有些讀者可能便會有這樣的疑問:
- 貪心法還有可能跟其他演算法結合嗎?
答案是肯定的,但其涉及的概念將會更深入一些。做為階段性的學習任務,我們就先在這裡停下來,讓讀者把目前階段的知識吸收完整後,未來就能夠更扎實的理解後續的延伸。
希望本章節能初步讓讀者認識到,在思考題目時不要總是往單一演算法或是資料結構去思考,而是將問題做出仔細的拆解後,逐步找出每一個部份分別需要用什麼樣的技巧擊破,才能夠設計出一個完整的演算法。
小智買了一個神奇的數字密碼鎖,這個數字密碼鎖總共有 $n$ 個介於 $1$ 到 $9$ 的正整數,每次調整密碼鎖上的數字時,必須一次調整其中連續的 $k$ 個數字,並且只能將這 $k$ 個數字分別調大一個數字。例如,若原來的數字是 $5$,則調整後變成 $6$,但若原來的數字是 $9$,則調整後的數字將變成 $1$。
因此,若 $n = 5$,且原來的這五個數字分別是 $1\ 2\ 3\ 4\ 9$。當 $k = 2$ 時,共有四種調整的方法,而調整後的結果共有四種可能,分別是 $2\ 3\ 3\ 4\ 9$、$1\ 3\ 4\ 4\ 9$、$1\ 2\ 4\ 5\ 9$、和 $1\ 2\ 3\ 5\ 1$。
給定 $n$ 和 $k$ 的值,已知目前數字密碼鎖上的 $n$ 個數字 $a_1, a_2, \ldots, a_n$,及解開密碼鎖所需要的 $n$ 個數字 $b_1, b_2, \ldots, b_n$,請計算小智最少需要調整幾次密碼鎖,才能將數字密碼鎖成功解開。
條件限制
- $10<n\leq 10000$
- $k < 100$
有一個電子寵物雞遊戲,遊戲軟體中會提供若干種食物,每種食物都有固定的熱量,並有其保存期限。從飼養電子寵物雞開始計時後,每分鐘內你可以從這些食物中選擇一種食物餵食寵物雞(一分鐘只能餵食一次,否則寵物雞會消化不良),但要注意不可餵食保存期限過期的食物,否則寵物雞會立刻暴斃。餵食後食物數量會自動減少,且每單位熱量會使你的寵物雞體重增加 $1$ 公斤;每達到 $1$ 分鐘沒有餵食,寵物雞體重會減少 $1$ 公斤。現在電子寵物雞公司為了促銷,特別辦了一個電子寵物雞飼養高手的比賽,給定一樣的食物種類、熱量、及保存期限,在比賽終止時間到達時,將其寵物雞的體重增加最多者將贏得冠軍。
請你寫出一個程式,由所給定的 $N$ 個食物的熱量和保存期限,以及比賽終止時間,找出一定可贏得冠軍的飼養方法之體重增加量。
條件限制
- $1\leq N \leq 10^5$
- 保證答案與給定的所有數字都在
int範圍內。
伊凡有 $n$ 個不同的盒子。其中第一個盒子包含了 $n$ 種不同顏色的球。他想進行一個奇特的遊戲,將這些球重新分配到盒子中,使得對於每個 $i (1 \leq i \leq n)$,第 $i$ 個盒子只包含第 $i$ 種顏色的所有球。
在每回合中,他會執行以下操作:
- 選擇任意一個非空的盒子,取出其中的所有球;
- 然後,選擇任意 $k$ 個空盒子(取出球後的盒子現在是空的,因此可以再次選擇它),將取出的球分成 $k$ 個非空的組,並將每組放入其中一個盒子。每個組必須放入不同的盒子中。這裡,$k$ 可以是 $2$ 或 $3$。
- 每回合的代價是他從盒子中取出球的數量。遊戲的總代價是伊凡完成所有操作直到所有球被正確分配所花費的總代價。
請幫助伊凡確定遊戲可能的最小總代價。
條件限制
- $1 \leq n \leq 2\times 10^5$
- $1\leq a_i\leq 10^9$,滿足 $a_i$ 是第 $i$ 種顏色球的數量。
自從小當家得到了傳說中的八樣廚具之後,回到了他母親的店——楊泉酒家。
由於大家都愛看中華一番的漫畫,所以有很多人慕名前往楊泉酒家吃飯。
楊泉酒家的廚房總共有 $k$ 個炒菜鍋,而客人可能點菜的種類有 $n$ 種。
由於小當家每次只能炒一道菜,而且一定要按照客人點菜的順序炒,必須要精簡洗炒菜鍋的次數,這樣才能加快速度。
是這樣的,一旦這次炒菜使用的炒菜鍋,沒有被用過,或者上一道菜與這一道菜種類不同,炒菜前就必須叫四郎先洗鍋子。
要不然被老饕們發現下場會很慘的。
這可讓在廚房裡負責洗鍋子的四郎大傷腦筋了,他看著已經依序點好的 $p$ 道菜餚,心裡一直盤算著,到底最少只要洗幾次鍋子呢?
請你寫個程式來回答這個問題吧!
條件限制
- $1\leq k\leq n\leq 10^5$
- $1\leq p\leq 5\times 10^5$
在一場電影祭中,有 $n$ 場電影即將上映。同時,abc 電影社有 $k$ 位成員要參加電影祭。
對於每一場電影,你都知道它的開始和結束時間,在每個人同一時刻只能看一部電影的條件下,請問 abc 電影社的 $k$ 位成員最多可以看到多少不同部的電影?
條件限制
- $1\leq k \leq n\leq 2\times 10^5$
- $1\leq 開始時間 < 結束時間 \leq 10^9$
為了了解一段古文在記錄些什麼,有 $M$ 位朋友來一起幫忙抄這些古文。
由於要確切記錄各個古文字出現的順序,所以每個人只能抄寫一段連續的文字,不能跳著抄寫。同時,由於每個古文字的寫法難度不同,如果分配不當的話會導致某些人的工作量太大。
為求公平起見,大家調查好了抄寫 $N$ 個古文所需要花的時間,並決定讓這 $M$ 個人每個人的工作量都不能超過某個上限 $X$,但同時這個人也必須把所有的古文字都抄寫完才算達成任務。你能寫個程式計算如何分配,讓 $X$ 值盡量小嗎?
條件限制
- $1\leq M\leq N\leq 10^5$
- 抄寫每個文字的工作量皆 $\leq 10000$。
你和對手各有 $N$ 匹馬,要進行 $N$ 場比賽。一匹馬只限出場一次,同場比賽中速度較快的馬獲勝。若兩匹馬速度一樣,則算平手。你可以決定你的馬匹的出場順序;而你的對手,就如同齊王,會在第一場比賽出速度最快的馬,第二場出次快的馬,…,第 $N$ 場出速度最慢的馬。
除此之外,你還可以決定比賽的時間,全部 $N$ 場比賽都會在你選的這一天進行。在比賽之前,勤勞的你每天都會訓練你的每一匹馬;而你的對手自我感覺非常良好,因此不會訓練他的馬。每一匹馬的素質不同,我們用 $a_i$ 來表示第 $i$ 匹馬的速度,用 $b_i$ 來表示第 $i$ 匹馬的成長率。經過 $m$ 天的訓練,你的第 $i$ 匹馬在第 $m+1$ 天的速度就會是 $a_i+m\times b_i$。對手的第 $j$ 匹馬在每一天的速度都是 $c_j$。
現在你有你和對手共 $2N$ 匹馬的資料,請決定訓練的天數 $M$,使得在第 $M+1$ 天比賽的時候,你有一個出場順序可以贏得 $N$ 場比賽中的至少 $K$ 場(不包含平手)。
條件限制
- $1\leq K\leq N\leq 10000$
- $0\leq a_i, c_j\leq 10^8$
- $0\leq b_i\leq 100$